Faleza

Cerință

Micul Ion tocmai ce a terminat Facultatea de Geologie și Geofizică și s-a angajat cartograf pentru un important om de afaceri.

Acest om de afaceri dorește amenajeze o plajă pe litoral, însă are o suprafață limitată de pămant la dispoziție pentru a face acest lucru.

Mai exact, el are la dispoziție un dreptunghi cu colțurile $(xStart,yStart)(xFinal,yFinal)$ în planul cartezian xOy. $(xStart,yStart)$ reprezintă punctul din stânga jos al dreptunghiului, iar $(xFinal,yFinal)$ punctul din dreapta sus.

În acest dreptunghi, marea este determinată de o ecuație matematică cunoscută.

Pentru exemplificare, fie ecuația polinomiala $f(x)=k_n \cdot x^n+k_{n-1} \cdot x^{n-1}+\ldots+k_1\cdot x^1+k_0$ care descrie marea și pe care o vom particulariza mai jos.

Tot ce se află deasupra sau pe graficul funcției se va afla pe uscat iar tot ce se află sub este în mare. În acest context, $x$ reprezintă abscisa unui punct în aceste coordonate.

De exemplu, pentru $f(x)=x^2-10\cdot x+1$ și punctul $(1,0)$ avem $1-10+1=-8 \lt 0 \Rightarrow$ punctul $(1,0)$ se află pe uscat.
Alt exemplu, pentru punctul $(10, -2)$ și aceeași mare avem $100-100+1=1\gt-2 \Rightarrow$ punctul se află în mare.

Funcțile care vor descrie funcția mării sunt:

• x (pentru polinom de gradul I);
• x^nr (pentru x la o anumită putere);
• sin(...) (pentru funcția sinus);
• cos(..) (pentru funcția cosinus);
• exp(...) (pentru funcția exponențială);
• ln(...) (pentru funcția logarithm);

Fiecare funcție poate fi combinată cu operațiile matematice standard(+,-,*,/) și cu niște constante iar sintaxa va fi corectă.
Spre exemplu 5x, 5*x, x*5*10 vor fi tot funcții polinomiale valide. Doar x5 nu va fi o funcție validă.
Aceste constante pot avea și paranteze, de exemplu (1/2)*x. Totodată, putem avea și semnul '-' în cazul în care înmulțim cu un număr negativ, de exemplu -1*x.
De asemenea, funcțiile pot fi și ele combinate cu operațiile matematice standard(+,-,*,/) și cu alte funcții sau pot fi puse ca argumente(intre paranteze).
Nu există spații in funcția mării.

Omul de afaceri dorește să determine o aproximare cât mai bună a raportului pământ/mare pentru a amenaja o plajă care să atragă cât mai mulți turiști. Astfel, i-a înmanat misiunea aceasta dificilă Micului Ion. Cum săracul Ion nu prea știe de unde să înceapă rezolvarea, vă roagă pe voi să îl ajutați să rezolve această problemă.

Cu toate acestea, afaceristul este un om nerăbdător, așa că el a pus la dispoziție și un schelet de cod. Așadar, în fișierul help.cpp veți găsi o funcție care să calculeze valoarea unei funcții matematice într-un anumit punct x, plus alte funcții care v-ar putea fi de ajutor. Tot în acest fișier veți găsi și un exemplu despre cum sa folosiți scheletul de cod. NU sunteți obligați să le folosiți, însă el s-a gândit că poate v-ar fi de ajutor.

Aveți de rezolvat, așadar, următoarea cerință: Aproximați raportul uscat/mare pentru întreg dreptunghiul. În secțiunea de restricții și precizări găsiți cum poate fi descrisă funcția mării.

Date de intrare

Fișierul faleza.in conține pe prima linie ecuația mării. Pe următoarea linie, coordonatele $(xStart,yStart)$ respectiv $(xFinal,yFinal)$ prin care este marcat dreptunghiul mare.
$(xStart,yStart)$ reprezintă colțul din stânga jos, iar $(xFinal,yFinal)$ colțul din dreapta sus.

Date de ieșire

Fișierul faleza.out va conține aproximarea raportului uscat/mare a dreptunghiului.

Restricții și precizări

• $xStart$, $xFinal$, $yStart$, $yFinal$ sunt numere intregi.
• $yStart, yFinal \geq 0$;
• $|yFinal-yStart| \cdot |xFinal-xStart| \leq 50$
• Dacă nu există uscat sau mare într-un dreptunghi, raportul va fi egal cu $0.00$.
• Funcția mării va avea cel mult $300$ de caractere.
• În funcția mării va conține doar numere intregi.
• Pentru $21$ de puncte funcția mării este descrisă de un polinom de gradul I.
• Pentru alte $17$ puncte, funcția mării este descrisă de o funcție strict polinomială oarecare;
• Pentru $33$ de puncte funcția mării poate conține funcțiile $\sin$, $\cos$ și alte combinații cu aceste funcții ($\sin$ de un polinom, $\cos$ de polinom, $\sin$ de $\cos$ etc.)
• Pentru $29$ de puncte funcția mării mai poate conține și funcția exponențială $e^x$, funcția logaritm și alte combinații de funcții($\sin$, $\cos$, polinoame)
• Aproximarea voastră trebuie să fie cu o eroare relativă mai mică decat $0.05$. Această eroare se calculează după cum urmează:

• Dacă răspunsul are o eroare de până în $0.1$, veti primi $50\%$ din valoarea testului.

Exemplul 1

faleza.in

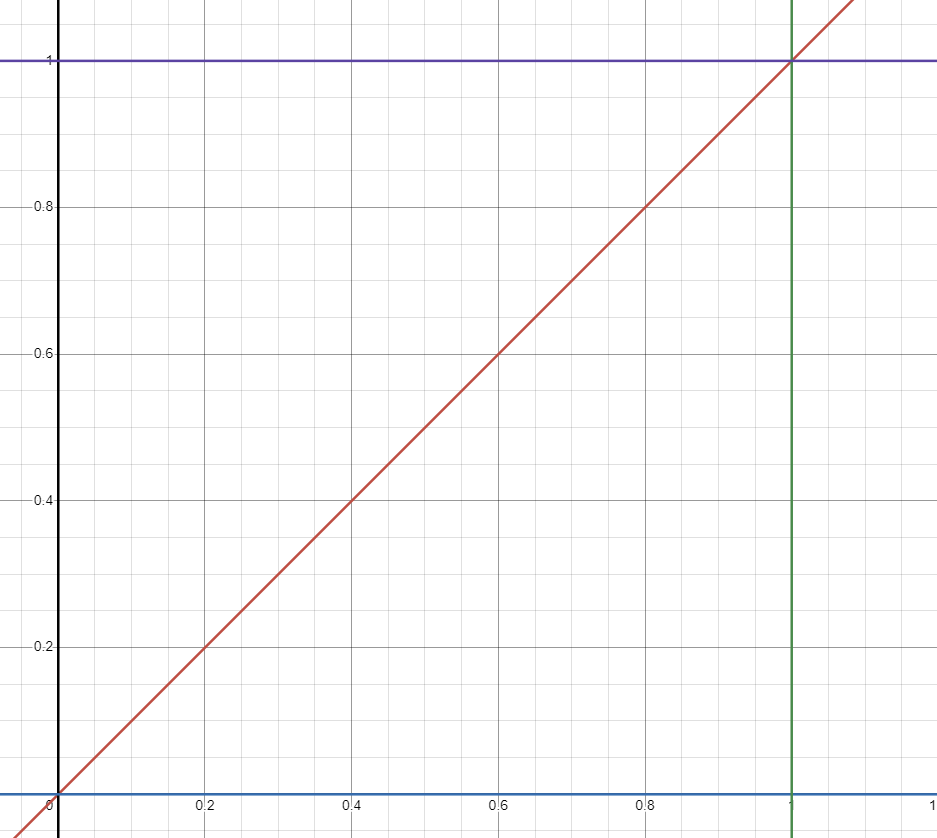
x 
0 0 1 1

faleza.out

1.0  

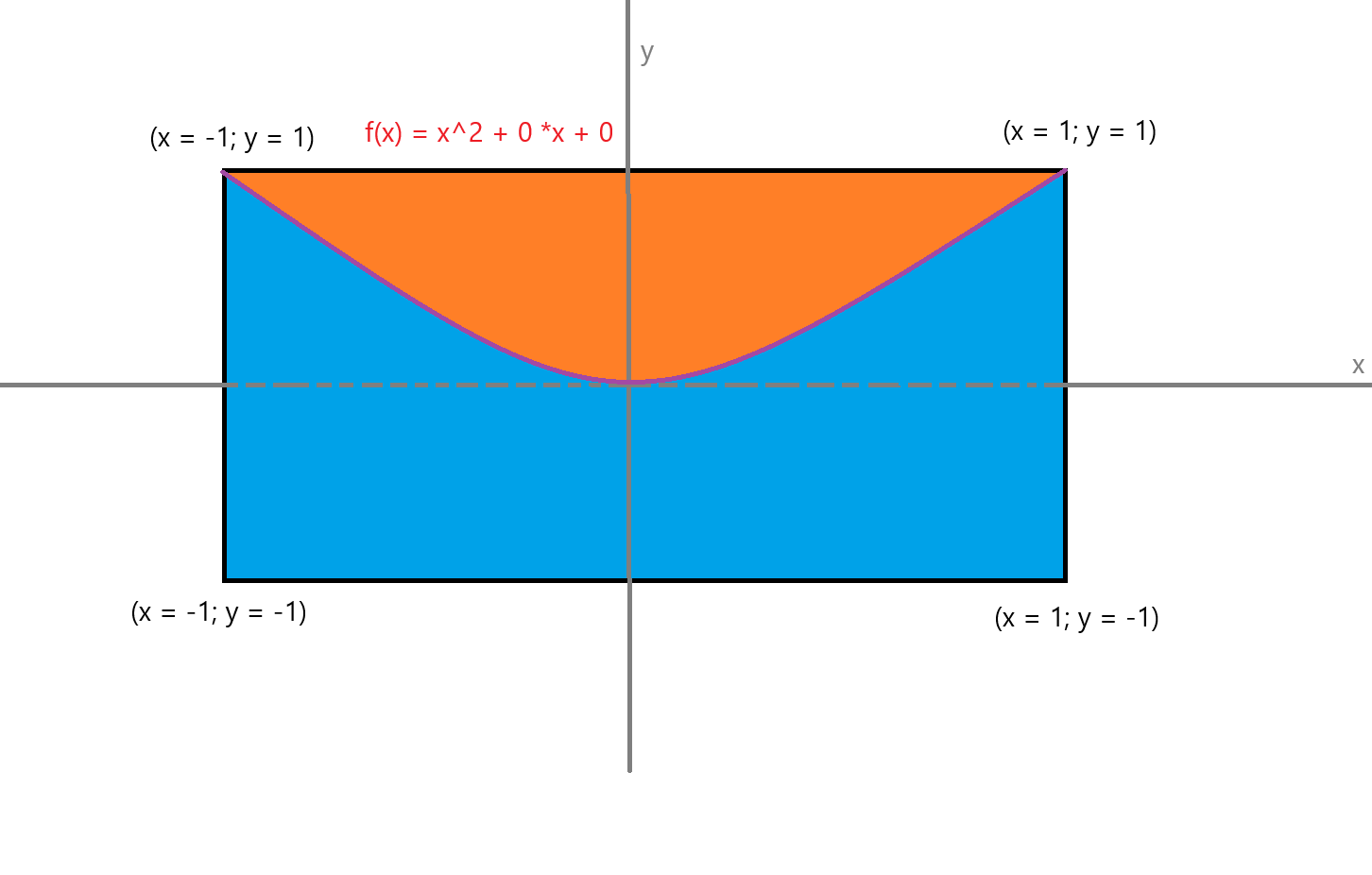
Explicație

Funcția $f(x) = x$ are următoarea formă în dreptunghiul $(0,0)(1,1)$:

Exemplul 2

faleza.in

sin(x) 
-2 1 -1 2

faleza.out

0.0

Explicație

Funcția $f(x) = \sin(x)$ este în totalitate sub dreptunghiul căutat.

Exemplul 3

faleza.in

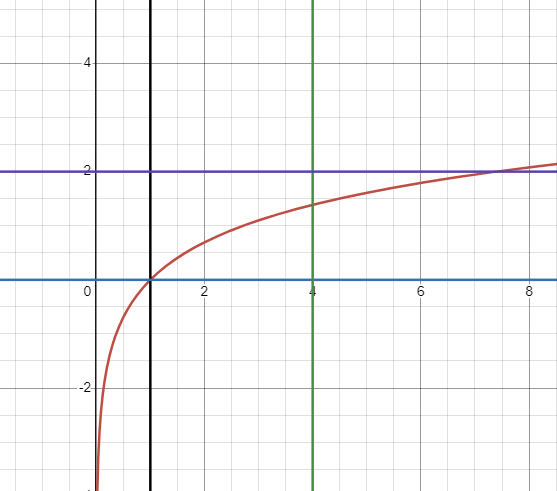
ln(x) 
1 0 4 2

faleza.out

1.35856

Explicație

Funcția $f(x) = \ln(x)$ arată astfel: