Lakeside Walk 2

Note the unusual memory limit for this problem.

Inspired by Carlo's success, Alessandro has decided to start his own software company in the mountains. However, unlike Carlo, he settled in a city where the weather is highly unpredictable.

Initially, the entire city is dry, but over the course of $Q$ days, rainfall and droughts will continuously change its conditions.

The city is represented as an $N \times M$ grid, with cells indexed from $(1,1)$ to $(N,M)$.

On day $i$ ($0 \le i < Q$), a rectangular region of the grid undergoes a weather change. Given integers $x_1$, $x_2$, $y_1$, $y_2$, all cells $(x,y)$ satisfying:

will switch their state -- wet cells become dry, and dry cells become wet.

At the end of each day, Alessandro wonders: What is the total perimeter of the wet regions? Unfortunately, he struggles to find this value. Can you help him determine the perimeter after each day's changes?

Input data

The input file consists of:

• item a line containing integers $N$, $M$, $Q$: $N$ and $M$ represent the size of the city, $Q$ represents the number of days.
• item $Q$ lines, with line $i$ consisting of integers $\mathtt{x_1}_{i}$, $\mathtt{x_2}_{i}$, $\mathtt{y_1}_{i}$, $\mathtt{y_2}_{i}$, representing the rectangular area that will change on day $i$.

Output data

The output file must contain a single line consisting of the $Q$ integers $P_{0}, \, \ldots, \, P_{Q-1}$.

Constraints and clarifications

• $1 \le N,M \le 1 \ 000 \ 000$.
• $N \cdot M \le 10 \ 000 \ 000$.
• $1 \le Q \le 200 \ 000$.
• $1 \le {x_1}_{i} \le {x_2}_{i} \le N$ and $1 \le {y_1}_{i} \le {y_2}_{i} \le M$ for each $i=0\ldots Q-1$.

Example

stdin

4 5 4
1 2 3 4
2 3 4 5
1 4 2 5
1 4 3 5

stdout

8
16
24
22

Explanation

In the first sample case the city is represented as a $4 \cdot 5$ grid, with $(1,1)$ being in the bottom left corner.

In the following figures, at the end of each day, the wet cells will be colored in blue, a red line will mark the perimeter of the wet regions, and a dashed black line will outline the region affected by a weather change.

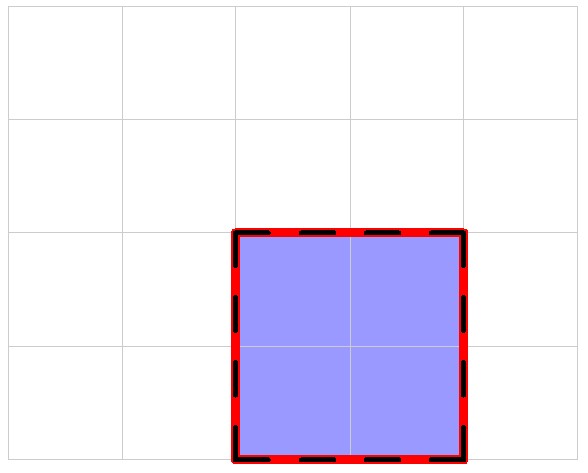
At the end of the first day, the total length of the perimeter is $8$.

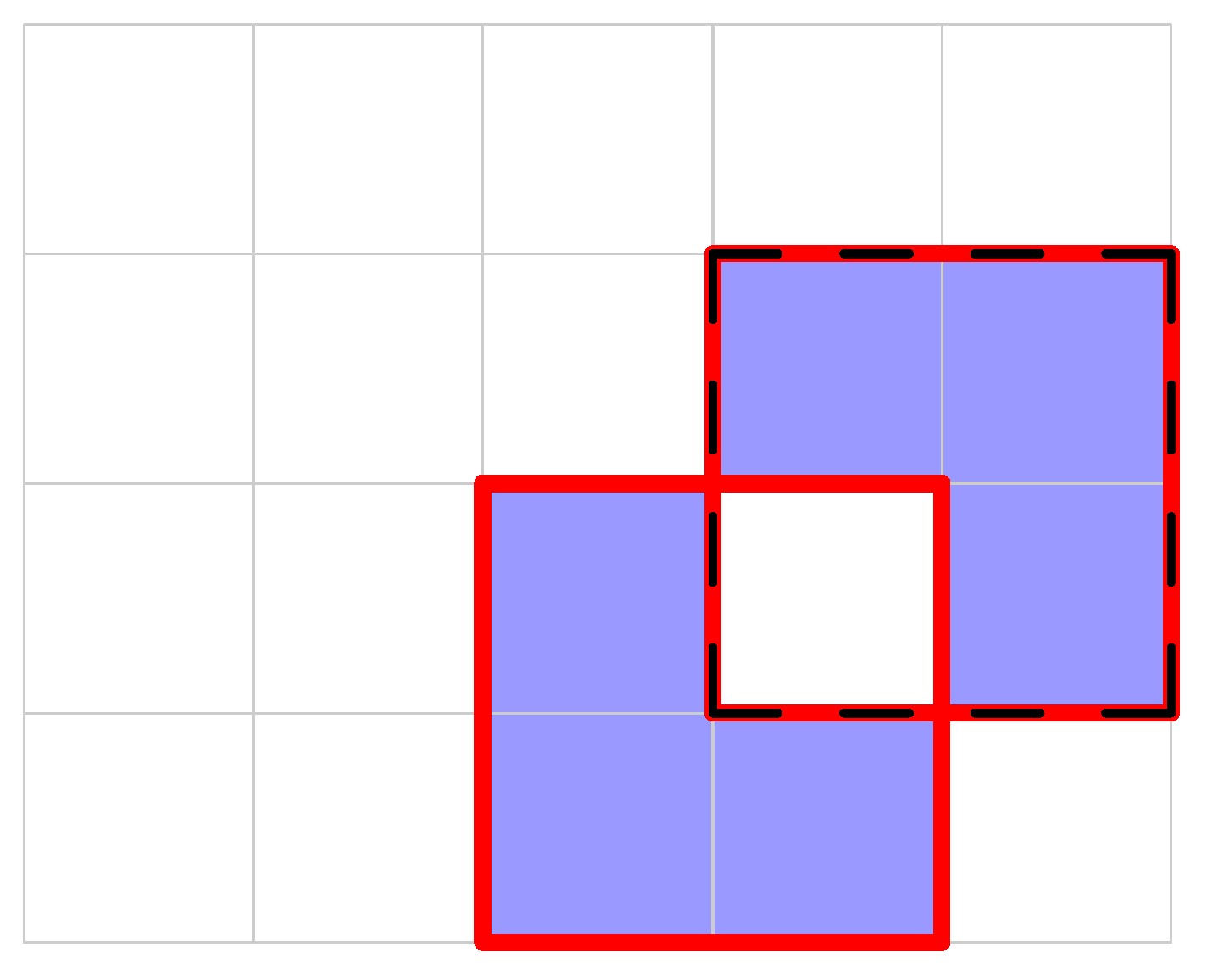
At the end of the second day, the total length of the perimeter is $16$.

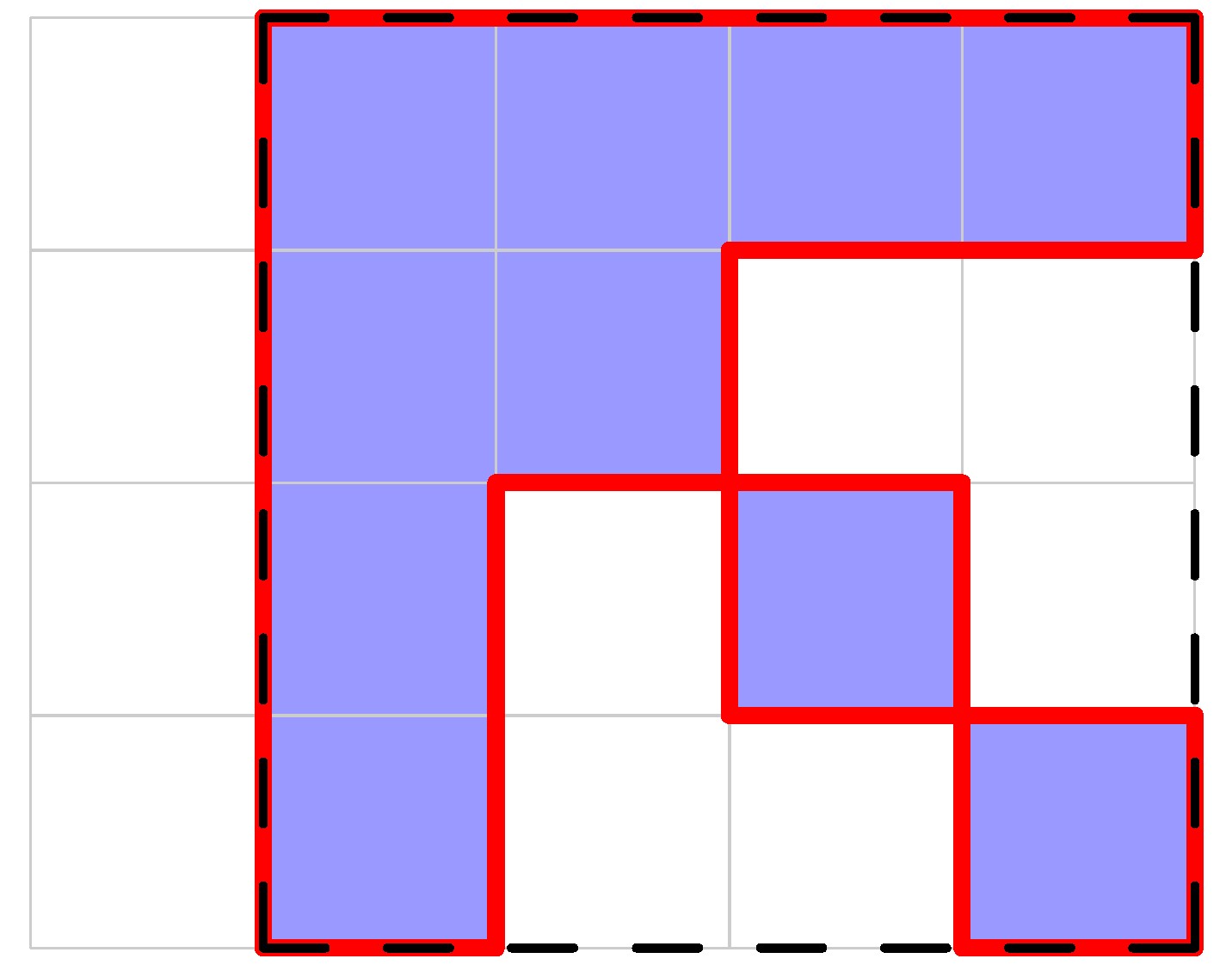
At the end of the third day, the total length of the perimeter is $24$.

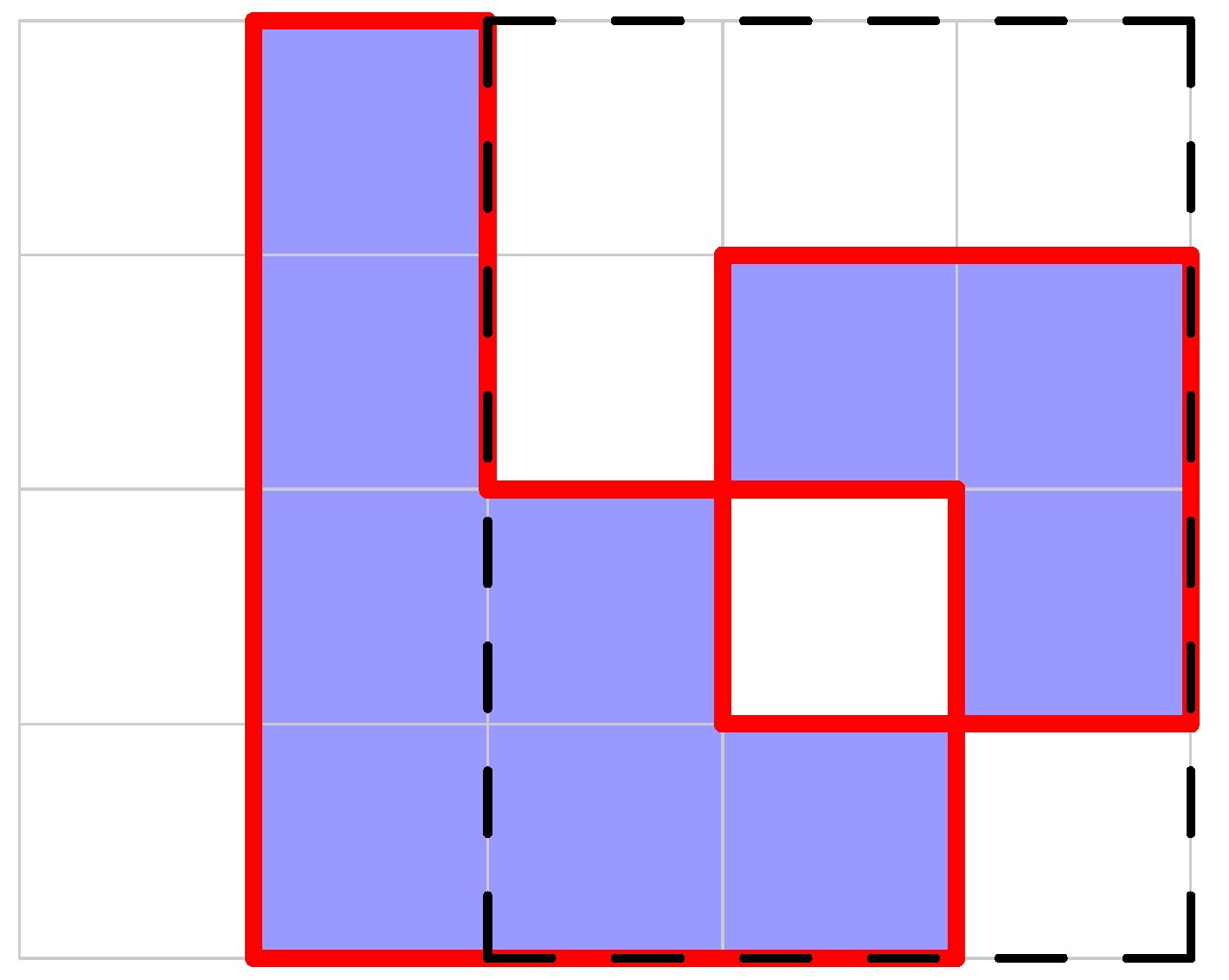
At the end of the fourth day, the total length of the perimeter is $22$.