Cerință
O matrice binară se numește conectată dacă se poate ajunge din orice valoare de în orice altă valoare de trecând doar prin valori de . O matrice care conține doar se consideră conectată.
Se dă o matrice binară (nu neapărat conectată). Să se găsească două matrici binare conectate și astfel încât să se respecte următoarea condiție: dacă și numai dacă .
Se garantează că matricea conține cel puțin un pe fiecare rând.
Date de intrare
Pe prima linie se vor afla valorile , (dimensiunile matricei). Următoarele linii conțin fiecare câte valori din mulțimea , reprezentând elementele matricei .
Date de ieșire
Dacă nu există soluție, se va afișa . Altfel, se va afișa matricea sub forma a linii conținând câte valori din mulțimea , apoi se va afișa matricea în același mod. Între cele două matrici se poate afișa un rând liber, chiar dacă nu este necesar.
Restricții și precizări
Pentru toate testele, se respectă .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 4 | Valorile de din sunt conectate și . |
| 2 | 7 | Valorile de din sunt conectate și . |
| 3 | 17 | |
| 4 | 21 | , iar matricea este o tablă de șah ( dacă și numai dacă și au parități diferite). |
| 5 | 51 |
Exemplul 1
stdin
4 4
0 1 0 1
0 0 1 0
0 1 0 1
1 1 1 0
stdout
0 1 1 1
0 1 0 0
0 1 1 1
1 1 1 0
0 0 1 0
0 1 1 0
0 0 1 0
0 0 0 0
Explicație
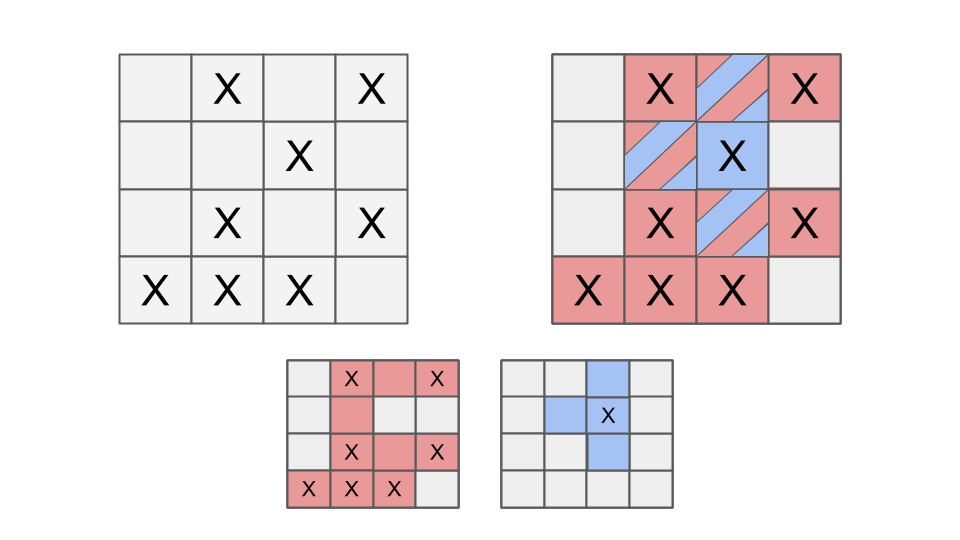
Exemplul este ilustrat în imaginea de mai sus. În stânga-sus este reprezentată matricea (celulele marcate cu 'X' conțin ). Jos sunt reprezentate cele două matrici și (celulele colorate conțin ). În dreapta-sus este reprezentată suprapunerea celor două matrici și . Se poate observa cum celulele marcate cu 'X' apar în exact una din matricile și , conform cerinței.
Acasta nu este unica soluție.
Exemplul 2
stdin
1 9
0 1 1 0 0 1 1 1 0
stdout
0 1 1 0 0 0 0 0 0
0 0 0 0 0 1 1 1 0
Explicație
Rândul liber dintre cele două matrici este opțional.
Exemplul 3
stdin
1 9
0 1 1 0 1 0 1 1 0
stdout
-1
Explicație
În acest caz, nu există soluție.