shell

Florin is again in Drobeta-Turnu Severin. Unfortunately, he did not get rid off the pickpockets that bother him so much! They followed him even in this beautiful city! But Florin is very smart and figured out how to get rid of them. Drobeta-Turnu Severin is a city that is represented by a directed acyclic graph with $n$ vertices and $m$ edges. To finally get rid of those annoying pickpockets, Florin (who is initially in vertex $1$) has to reach vertex $n$ using a certain path. He managed to obtain a list of $p$ vertices. In his way from vertex $1$ to vertex $n$ he has to cross all these $p$ nodes in the given order, or else he will not get rid of the pickpockets and our hero will be very upset.

Task

Find the number of possible paths from vertex $1$ to vertex $n$ that cross all $p$ vertices in the given order from the list. Because the result can be very big you have to print the answer modulo $1 \ 000 \ 000 \ 007$.

Input

The first line contains three integers $n$, $m$ and $p$.

The second line contains the $p$ vertices that have to be crossed by Florin in the given order.

The next $m$ lines contain the edges from the graph, represented by two integers $x$ and $y$, meaning there is an edge from vertex $x$ to vertex $y$.

Output

The first line will contain only one integer representing the number of paths modulo $1 \ 000 \ 000 \ 007$.

Restrictions

• WARNING! There can be more edges between the same 2 vertices!!!!
• WARNING! It can be observed that at subtask 3, $m$ is bigger than at the subtask.
• You have to print the answer modulo $1 \ 000 \ 000 \ 007$.
• We had no good reason to name this problem shell.

Example

stdin

6 9 3
3 5 6
1 3
1 3
1 2
2 3
2 4
3 4
3 5
4 5
5 6 

stdout

6

Explanation

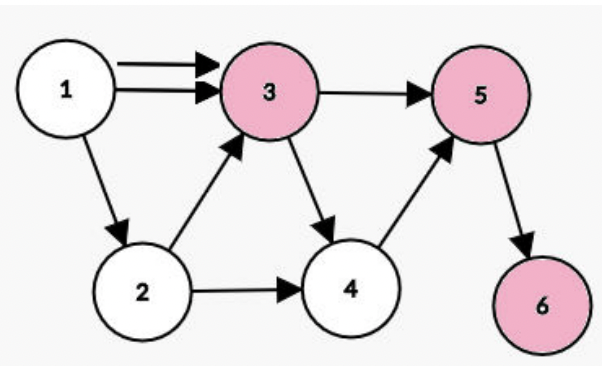
The $6$ paths are:

1. $1 \to 3 \to 5 \to 6$
2. $1 \to 3 \to 4 \to 5 \to 6$
3. $1 \to 3 \to 5 \to 6$
4. $1 \to 3 \to 4 \to 5 \to 6$
5. $1 \to 2 \to 3 \to 5 \to 6$
6. $1 \to 2 \to 3 \to 4 \to 5 \to 6$

It can be observed that $1 \to 3 \to 4 \to 5 \to 6$ appears $2$ times, this is because there are $2$ edges from $1$ to $3$. One of the paths use an edge, the second one uses the other edge. The same situation is for $1 \to 3 \to 5 \to 6$.