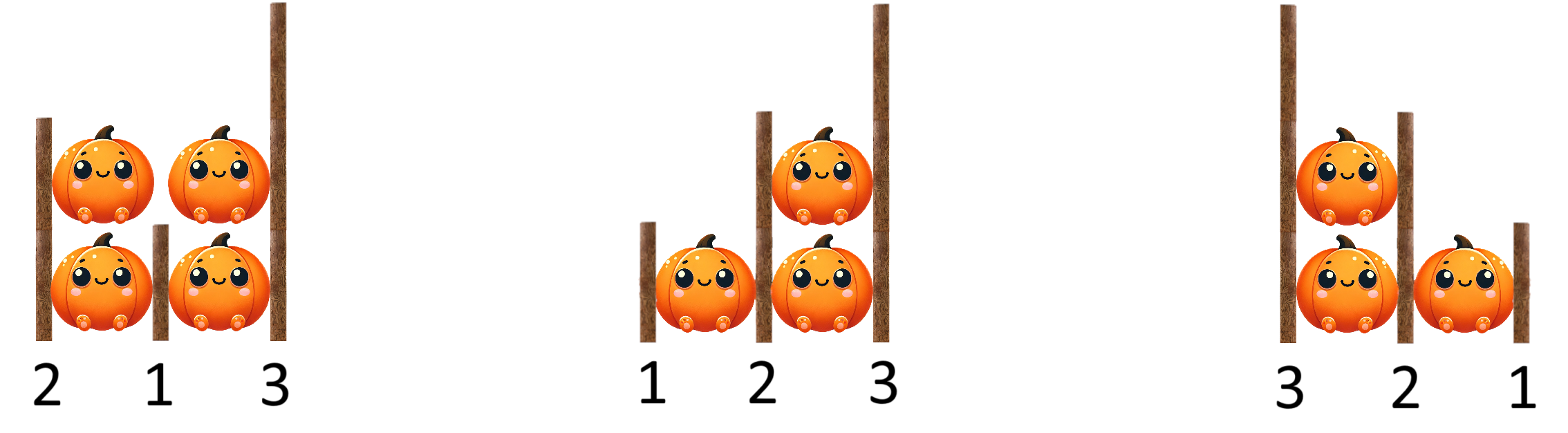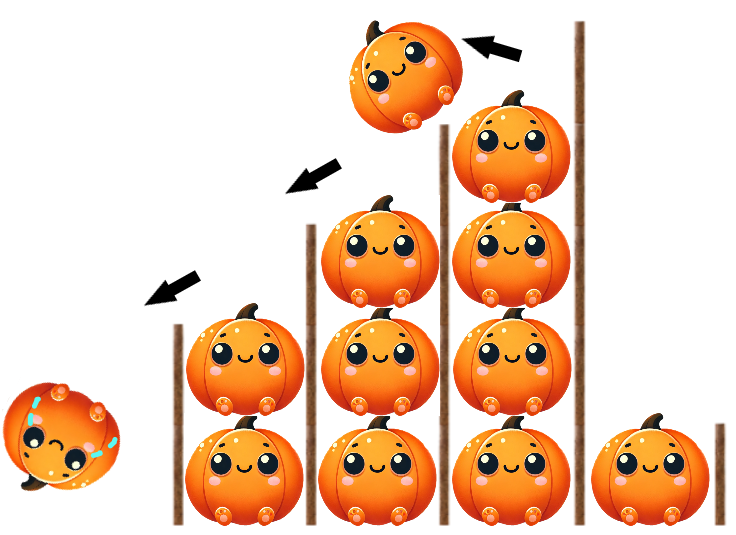
Vlad și Andrei vor să decoreze grădina în spiritul Halloween-ului și au la dispoziție o grămadă de dovleci sculptați! Ei ar vrea să facă un perete de turnuri de dovleci și pentru stabilitatea aranjamentului ei au la dispoziție pari de lemn cu înălțimi distincte de la la .
Dovlecii se așază între pari, unul deasupra celuilalt, formând turnuri. Un turn de dovleci de înălțime este stabil dacă și numai dacă atât în stânga, cât și în dreapta sa, (dar nu neapărat imediat adiacent) se află cel puțin un par de înălțime mai mare sau egală cu . Deoarece au comandat un număr puțin cam mare de dovleci, Vlad și Andrei ar vrea să facă aranjamentul folosind cât mai mulți dovleci cu putință, urmând ca din restul să facă plăcinte.
Din păcate, ei mai trebuie să respecte și următoarea regulă atunci când așază parii: numărul de perechi de pari diferiți pentru care parul mai înalt este așezat înaintea parului mai mic trebuie să fie exact . O astfel de situație se numește o inversiune.
Cerință
Pentru din punctaj, se cere să se determine corect doar numărul maxim de dovleci ce pot fi folosiți astfel încât așezarea celor pari să aibă exact inversiuni. Adițional, pentru punctajul maxim, se cere să se afișeze o astfel de așezare a parilor.
Date de intrare
Intrarea constă dintr-o singură linie ce conține 2 întregi reprezentând și .
Date de ieșire
Afișați pe prima linie a ieșirii un singur număr întreg reprezentând numărul maxim de dovleci ce poate fi folosit în aranjament.
Pentru a obține punctajul complet, pe a doua linie a ieșirii afișați numere separate prin spații reprezentând un model de aranjament al parilor cu inversiuni care ține număr maxim de dovleci.
Restricții și precizări
- Dacă există mai multe aranjamente ce corespund, se poate afișa oricare.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 14 | |
| 2 | 15 | |
| 3 | 19 | |
| 4 | 12 | |
| 5 | 17 | |
| 6 | 23 | Fără restricții adiționale. |
Exemplul 1
stdin
3 1
stdout
4
2 1 3
Exemplul 2
stdin
3 0
stdout
3
1 2 3
Exemplul 3
stdin
3 3
stdout
4
3 2 1
Explicații pentru exemple