Buildings

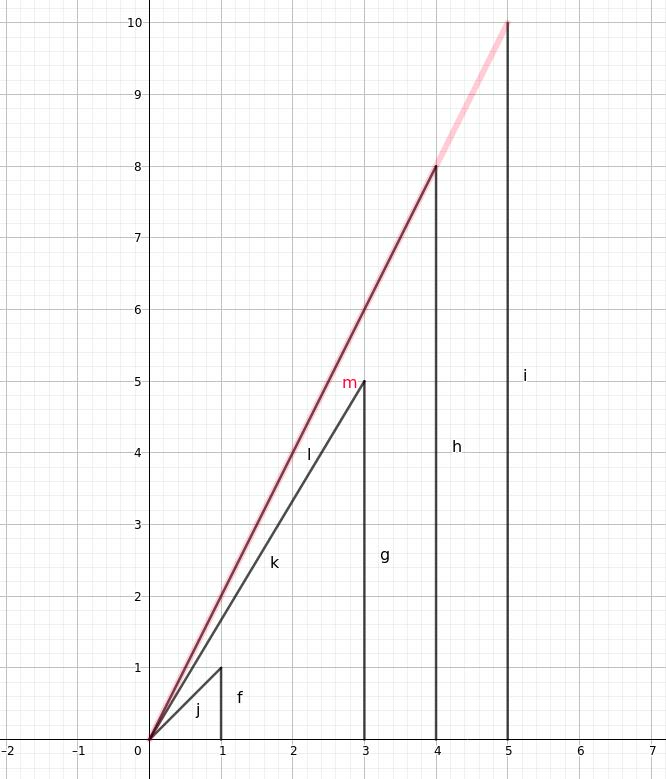
The mayor of Julc-Acopan wishes to be able to see as many buildings as he can from his home. His view of the town may be simplified to points on the plane. He is sitting at the origin at $(0, \ 0)$ and the buildings are segments from $(x_i, \ 0)$ to $(x_i, \ y_i)$. It is known that $x_i = i$, in other words $x_1 = 1, x_2 = 2$ and so on (the buildings occupy the integers $1, 2, ..., n$ on the $OX$ axis).

The mayor being mayor he may choose to destroy at most one building to accomplish his dream. You are asked to answer the maximum number of buildings he might see.

A building is considered seen if an area larger than $0$ is able to be seen, in other words if a single point is within sight it does not count.

Input

The first line contains the integer $n$, the number of buildings $(1 ≤ n ≤ 2 \cdot 10^5)$.

The following line contains $n$ integers each the $y_i$ ($1 ≤ y_i ≤ 10^{12}$), where $y_i$ is the value of building $i$.

For tests worth $20$ points it is guaranteed that $(1 ≤ n ≤ 1 \ 000)$.

Output

Output a single integer, the maximum number of buildings the mayor can see.

Example

stdin

5
1 4 5 8 10

stdout

3

Explanation

The mayor can demolish the second building and see the first, third and fourth building. The fifth building cannot be seen because only one point is within sight.

The following image may be of help