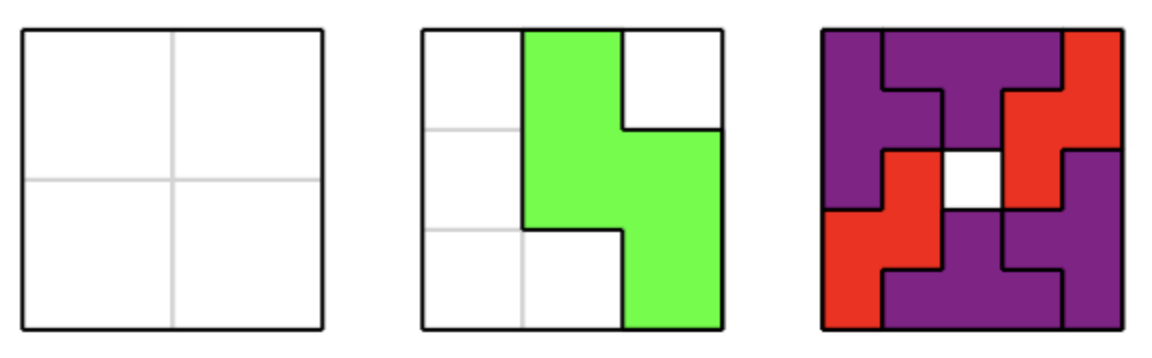
You are given an integer . You also have an empty grid of cells, on top of which you can add tetris pieces in the following way:
- Select cells from the grid which correspond to one of the following shapes:
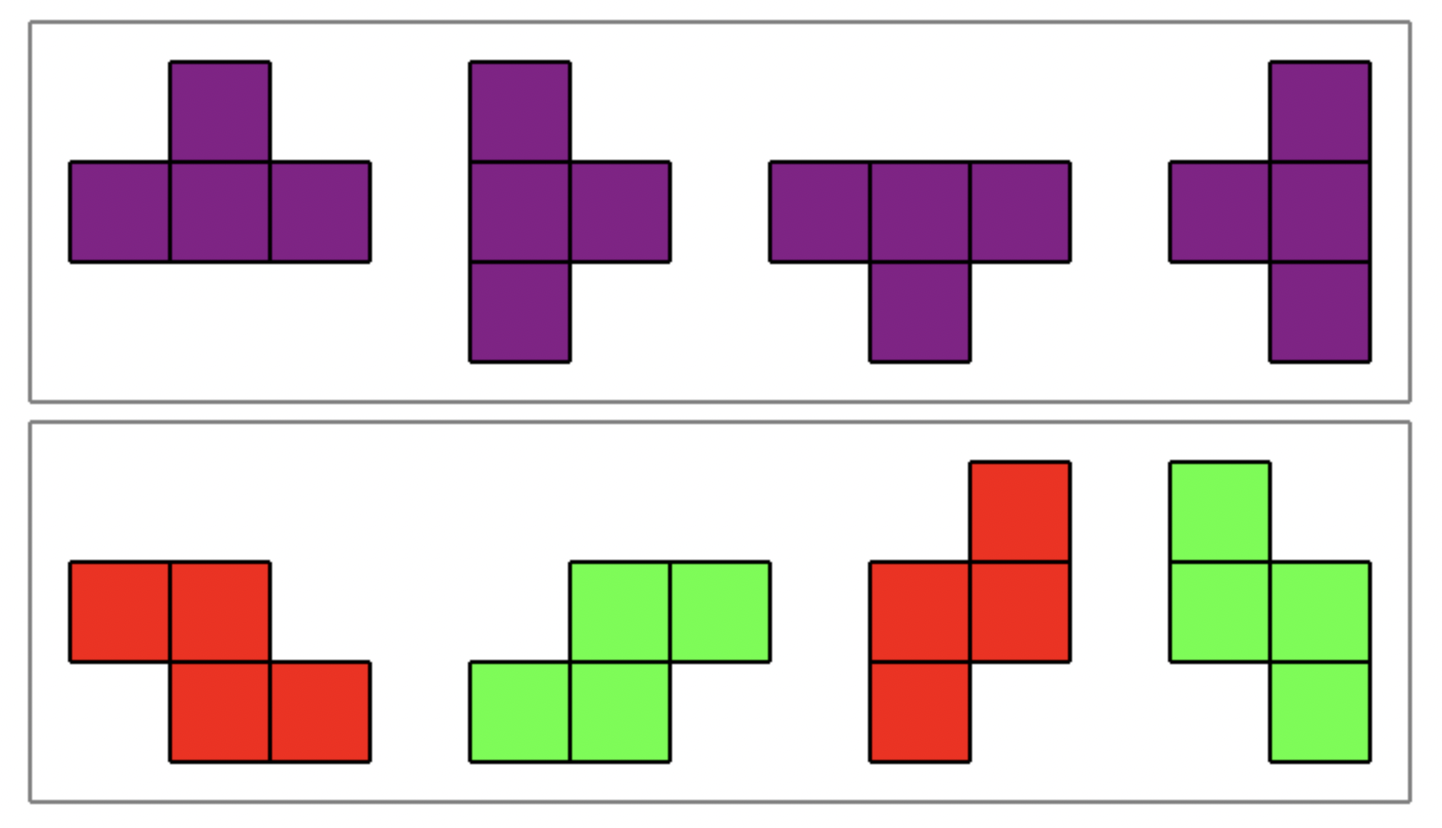
- If all selected cells are empty, then a new tetris piece is placed on top of them.
Any grid obtained through these operations starting from an empty grid is called a tetris tiling.
Task
Find any tetris tiling which uses the maximum possible number of pieces.
Input data
The first and only line of input contains a single integer , the size of the grid.
Output data
First, output one line containing one integer indicating the maximum number of tetris pieces that can placed on an grid.
Then, output lines, each containing space-separated integers. The -th integer of the -th line is denoted by .
If then the cell in row and column belongs to piece . Otherwise, if is , the corresponding cell is empty and does not belong to any piece.
If there are multiple solutions which maximizes the number of pieces in the tiling, output any of them.
Constraints and clarifications
| # | Points | Constraints |
|---|---|---|
| 1 | 25 | |
| 2 | 25 | |
| 3 | 50 |
Example 1
stdin
2
stdout
0
0 0
0 0
Example 2
stdin
3
stdout
1
0 1 0
0 1 1
0 0 1
Example 3
stdin
5
stdout
6
1 2 2 2 3
1 1 2 3 3
1 6 0 3 4
6 6 5 4 4
6 5 5 5 4
Explanation
It can be proven that for these values of , there are no tetris tilings that use more pieces than the ones depicted below.