
Carlo is a big fan of progressive music and he recently found out that progressive paintings exist too! Clearly, he wants to dive into it, therefore he hired you as his assistant. A progressive painting is made using Vim, and consists of a rectangle of coloured square cells. Since Carlo wants to be even more progressive, he only uses the colors red, green, and blue.
Carlo has a weird way of judging the beauty of his works. He invented a measure called -beauty. A square of size (that is, consisiting of contiguous cells of the painting) is beautiful if it contains an equal number of red, green, and blue cells. The -beauty of the painting is the number of beautiful squares of size in it.
Task
Carlo asked you a question to test your skill. Given , , and , does a painting with rows, columns, and an -beauty equal to exist? If so, could you paint one for him?
Input data
The input file consists of a single line, containing the integers , , , and .
Output data
If it is possible to produce a suitable painting, you have to output lines:
- One line containing the string
YES. - lines, each containing a string of length , consisting of
R,G, andBonly, representing red, green, and blue cells in the painting.
If it is not possible to do so, you have to output a single line containing the string NO.
Constraints and clarifications
| # | Points | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 30 | |
| 3 | 50 | |
| 4 | 20 | No additional constraints |
Example 1
stdin
4 3 2 4
stdout
NO
Explanation
It is not possible to make a painting satisfying the constraints.
Example 2
stdin
4 4 3 2
stdout
YES
RBRR
BGGB
GRBG
RBBG
Explanation
One possible painting, represented in the output, is the following:

It contains squares of size , that are the following:
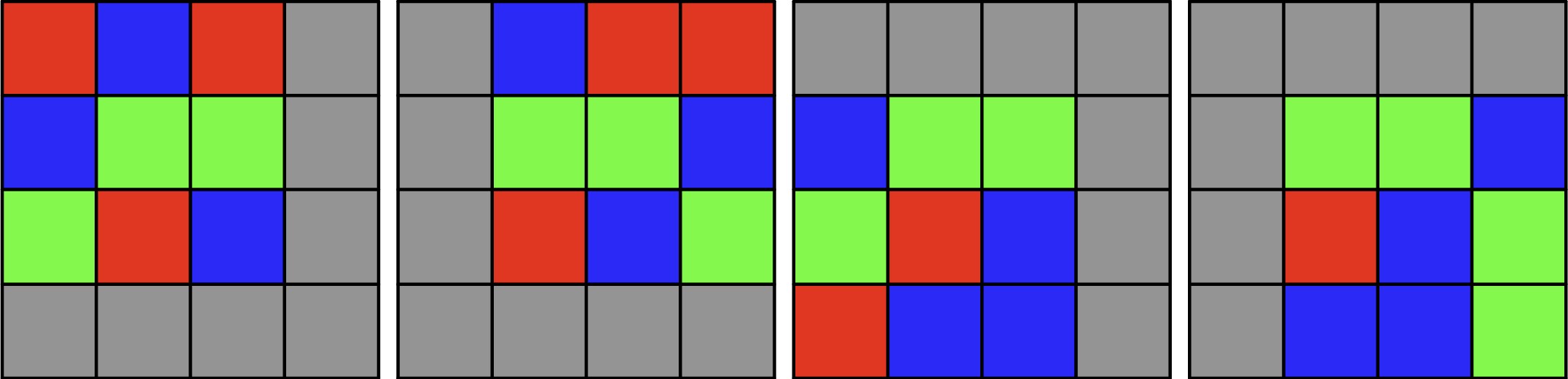
Only the first of them contain the same amount of red, green and blue cells. Hence, the painting satisfies Carlo's request.