Pavari

Cerință

Avem o placă dreptunghiulară cu $n$ linii și $m$ coloane, formată din $n \times m$ pătrățele de latură unitate. Dorim să pavăm complet această placă, având la dispoziție pavele din următoarele $4$ tipuri:

Tip	Imagine	Descriere
Tipul 1		Acest tip de pavea fiind simetrică la oricare dintre rotiri, are un singur mod în care poate fi pusă.
Tipul 2		Acest tip de pavea are două poziții în care poate fi pusă (orizontal sau vertical).
Tipul 3		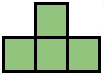Acest tip de pavea are $4$ poziții în care poate fi pusă.
Tipul 4		Acest tip de pavea are un singur mod în care poate fi pusă.

Paveaua de tip $4$ poate fi folosită cel mult o dată în orice test. Pentru celelalte $3$, se indică la fiecare test care dintre ele pot fi folosite (de $0$ sau mai multe ori).
Două soluții de pavare $A$ și $B$ diferă dacă există cel puțin o poziție pe placa dată care în soluția $A$ face parte dintr-un tip de pavea și în soluția $B$ face parte din alt tip de pavea sau dacă acea poziție face parte din același tip de pavea dar în soluția $A$ paveaua are altă orientare decât în soluția $B$.

Date de intrare

Fișierul pavari.in are pe prima linie numerele $n$ și $m$, reprezentând dimensiunile plăcii de pavat. Pe linia a doua se află un număr $p$, cuprins între $1$ și $3$ reprezentând numărul de tipuri de pavele care pot fi folosite. Pe linia următoare se află $p$ valori distincte, cuprinse între $1$ și $3$, scrise în ordine crescătoare, reprezentând tipurile de pavele.

Date de ieșire

Fișierul pavări.out are pe prima linie un număr natural reprezentând numărul de păvări distincte posibile.

Restricții și precizări

• $1 \leq n, m \leq 10$;
• $1 \leq n \times m \leq 50$;
• Pavela de tip $4$ poate fi folosită în orice test cel mult o dată.
• La orice soluție, pavelele trebuie să se afle integral în interiorul plăcii și să nu se suprapună.

Exemplu

pavari.in

2 6
3
1 2 3

pavari.out

3

Explicație

Culorile nu sunt importante, au fost adăugate doar pentru a diferenția tipurile de pavele.
Se pot folosi pavele de toate tipurile. Se observa ca nu se poate face nicio pavare folosind tipurile $3$ si $4$.