Sashka is responsible for the maintenance of the flowers in the city garden. The garden consists of flower beds, numbered with the integers from to , where some of the flower beds are connected by pipes. The beds and the pipes form a connected, acyclic, undirected graph, in which the flower beds are the nodes and the pipes -- the edges. In each bed there is an installed pump which can pump water from the underground. This water irrigates the bed in which the pump is located and sends water through the pipes to some of the beds that have a path of pipes to them. The pumps are numbered from to , with one pump's number being equal to the number of the bed it is located in. If the pump located in a bed with number () works for minutes, the water will reach all beds that have distance within edges from in the acyclic graph. The system of pumps is such that one pump runs first, then another one and so on. Two pumps never work simultaneously. A pump can run only once. A flower bed is considered irrigated if water has reached it, regardless of which pump. The pumps are designed in such a way, that if a pump with number runs, it should run at most minutes, otherwise it can malfunction. A run of a pump must continue an integer number of minutes. The pumps are identical and consume electricity as follows: minute run costs euro, minute run costs euro and so on. If a pump doesn't run, it won't consume electricity. Sashka is given the task of determining the minimum amount of money for electricity, when an appropriate set of pumps runs, so all the flower beds can be irrigated.
Task
Write a program which solves the task Sashka is given.
Input
The first line of the standard input contains an integer , equal to the number of beds (and pumps) in the garden. The second line contains also non-negative integers , separated by intervals -- the money for electricity, which a pump consumes for respectively minute run. The third line contains non-negative integers , separated by intervals -- the maximum allowed run time for each pump. If some of these integers is equal to , this means that the respective pump cannot be used. Each of the last lines of the standard input contains two positive integers and , defining a pipe (edge) connecting the beds with numbers and . It's guaranteed that the flower beds and the pipes, connecting them, form a connected, acyclic graph.
Output
On the only line of the standard output, the program should output the minimum amount of money for electricity so all the flower beds can be irrigated. If it's impossible to irrigate all the flower beds, your program should output .
Constraints
- Note: A graph is a chain if and only if each node has at most neighbors and there are exactly vertices with neighbor.
Subtasks
Subtask 1 (0 points)
- Sample test cases
Subtask 2 (11 points)
Subtask 3 (12 points)
- The graph is a chain
Subtask 4 (11 points)
- The graph is a chain
Subtask 5 (13 points)
- The graph is a chain
Subtask 6 (17 points)
Subtask 7 (14 points)
Subtask 8 (22 points)
Examples
stdin
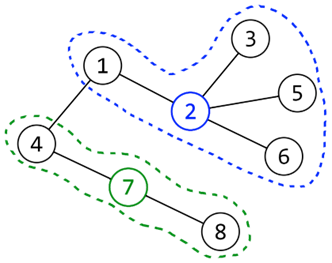
8
1 4 9 16 25 36 49 64
1 5 1 1 0 0 5 0
1 2
2 3
1 4
2 5
2 6
4 7
7 8
stdout
8
stdin
7
1 4 9 16 25 36 49
0 5 5 0 0 0 0
1 2
2 4
1 3
1 5
3 7
3 6
stdout
13
Explanation
Example №1: An irrigation with a minimum amount of money is achieved when pump № runs for minutes and pump № runs for minutes. The consumed electricity will cost euro.
Example №2: An irrigation with a minimum amount of money is achieved when pump № runs for minutes and pump № runs for minutes. The consumed electricity will cost euro.
Below are diagrams illustrating the graphs from the examples.