Problem 333: garden

Sashka is responsible for the maintenance of the flowers in the city garden. The garden consists of $N$ flower beds, numbered with the integers from $1$ to $N$ , where some of the flower beds are connected by pipes. The beds and the pipes form a connected, acyclic, undirected graph, in which the flower beds are the nodes and the pipes -- the edges. In each bed there is an installed pump which can pump water from the underground. This water irrigates the bed in which the pump is located and sends water through the pipes to some of the beds that have a path of pipes to them. The pumps are numbered from $1$ to $N$ , with one pump's number being equal to the number of the bed it is located in. If the pump located in a bed with number $x$ ( $1 \leq x \leq N$ ) works for $p$ minutes, the water will reach all beds that have distance within $p - 1$ edges from $x$ in the acyclic graph. The system of pumps is such that one pump runs first, then another one and so on. Two pumps never work simultaneously. A pump can run only once. A flower bed is considered irrigated if water has reached it, regardless of which pump. The pumps are designed in such a way, that if a pump with number $m$ runs, it should run at most $t_{m}$ minutes, otherwise it can malfunction. A run of a pump must continue an integer number of minutes. The pumps are identical and consume electricity as follows: $1$ minute run costs $c_{1}$ euro, $2$ minute run costs $c_{2}$ euro and so on. If a pump doesn't run, it won't consume electricity. Sashka is given the task of determining the minimum amount of money for electricity, when an appropriate set of pumps runs, so all the flower beds can be irrigated.

Task

Write a program which solves the task Sashka is given.

Input

The first line of the standard input contains an integer $N$ , equal to the number of beds (and pumps) in the garden. The second line contains also $N$ non-negative integers $c_{1},c_{2},\ldots,c_{N}$ , separated by intervals -- the money for electricity, which a pump consumes for respectively $1,2,\ldots,N$ minute run. The third line contains $N$ non-negative integers $t_{1},t_{2},\ldots,t_{N}$ , separated by intervals -- the maximum allowed run time for each pump. If some of these integers is equal to $0$ , this means that the respective pump cannot be used. Each of the last $N - 1$ lines of the standard input contains two positive integers $u$ and $v$ , defining a pipe (edge) connecting the beds with numbers $u$ and $v$ . It's guaranteed that the flower beds and the pipes, connecting them, form a connected, acyclic graph.

Output

On the only line of the standard output, the program should output the minimum amount of money for electricity so all the flower beds can be irrigated. If it's impossible to irrigate all the flower beds, your program should output $- 1$ .

Constraints

$1 \leq N \leq 2\ 000$
$0 \leq c_{i} \leq 10^{6}$
$0 \leq t_{i} \leq N$
Note: A graph is a chain if and only if each node has at most $2$ neighbors and there are exactly $2$ vertices with $1$ neighbor.

Subtasks

Subtask 1 (0 points)

Sample test cases

Subtask 2 (11 points)

$N \leq 8$

Subtask 3 (12 points)

$N \leq 75$
The graph is a chain

Subtask 4 (11 points)

$N \leq 500$
The graph is a chain

Subtask 5 (13 points)

$N \leq 2 \ 000$
The graph is a chain

Subtask 6 (17 points)

$N \leq 75$

Subtask 7 (14 points)

$N \leq 500$

Subtask 8 (22 points)

$N \leq 2 \ 000$

Examples

stdin

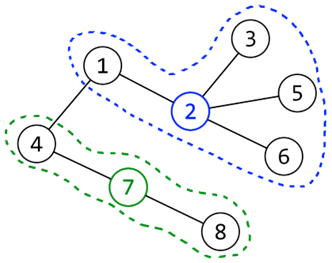
8                   
1 4 9 16 25 36 49 64
1 5 1 1 0 0 5 0     
1 2                 
2 3                 
1 4                 
2 5                 
2 6                 
4 7                 
7 8

stdout