A nice octagon is a convex figure with nonzero area with at most edges, where each edge is either parallel to the coordinate axes, or makes a angle with them. All edges parallel to the coordinate axes must have integer lengths; all other edges must have lengths that are integer multiples of . Below we can see a few examples of nice octagons.
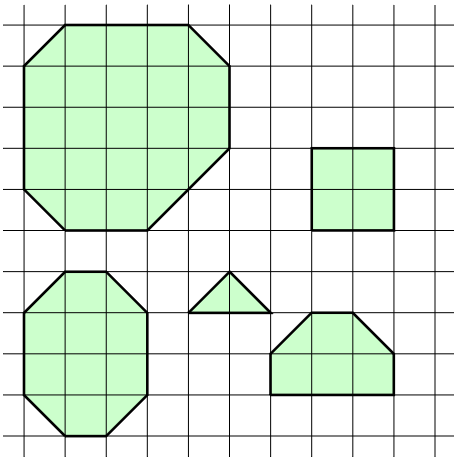
Suppose we walk around the edges of a nice octagon in counter-clockwise order. We observe that it is formed out of length and segments that join two
grid points that are consecutive in the walk. Consequently, the segments are split into different categories, depending on the direction in which they go: north, north-east, east, south-east, south, south-west, west, and north-west.
Task
Suppose you are given the maximum number of segments of each category that you can use. How many different nice octagons can you form?
Input data
The first and only line of the input contains 8 space-separated integers - the maximum number of segments going in the north, north-east, east, south-east, south, south-west, west, and north-west directions.
Output data
Output the required count of nice octagons, modulo .
Constraints and clarifications
- Let be the maximum of the eight values in the input.
- Two nice octagons are considered the same if one can be obtained from the other by a translation but without using rotations. In particular, two nice octagons are the same if and only if they use the same number of segments of each of the eight types.
| # | Points | Restrictions |
|---|---|---|
| 1 | 9 | There are no diagonal segments available. |
| 2 | 17 | |
| 3 | 29 | |
| 4 | 29 | |
| 5 | 16 | No further restrictions. |
Example 1
stdin
1 0 1 0 1 0 1 0
stdout
1
Explanation
In the first example, the only nice octagon is a square.
Example 2
stdin
1 1 1 1 1 1 1 1
stdout
19
Explanation
In the second example, there are nice octagons.
Example 3
stdin
2 2 2 2 2 2 2 2
stdout
228
Example 4
stdin
1 2 3 4 4 3 2 1
stdout
135
Example 5
stdin
100 100 100 100 100 100 100 100
stdout
636061137