railroad

Task

There are $N$ cities and $M$ bidirectional railways connecting cities $a_i$ and $b_i$ with a travel time of $c_i$ minutes. There is also a train that connects city $0$ with city $N-1$, this train will always take the only shortest path between the two cities.

However, the train only passes through some cities and the mayors of the cities it doesn't pass through are angry.

To please the mayors, you can upgrade a single railway to high-speed railway, which will reduce the travel time by $1$ minute for each euro spent. Of course, the travel time must be strictly positive after the upgrade.

You want to upgrade a railway so that the new shortest path between city $0$ and city $N-1$ always passes to at least a city that wasn't passed by the train before.
In the new railway network there may be many shortest paths, however the original one must not be one of them.

What is the minimum amount of money you need to spend to achieve this?

Input

The first line contains the integers $N$ ($2 \le N \le 10^5$) and $M$ ($1 \le M \le 3 * 10^5$), the number of cities and the number of railways.

The following $M$ lines contains three integers $a_i$, $b_i$ and $c_i$ representing a bidirectional railway between $a_i$ and $b_i$ with a travel time of $c_i$ minutes. ($0 \le a_i, b_i \le N - 1$), ($1 \le c_i \le 10^9$).

It is guaranteed that the shortest path between 0 and $N-1$ is unique.

For tests worth $35$ points, ($N \le 1000$, $M \le 2000$).

For tests worth $30$ more points, $N = M$, and each city has exactly two railways.

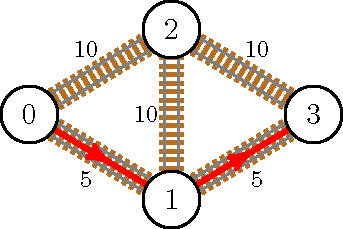
Example 1

stdin

4 5
0 1 20
0 2 60
1 2 5
2 3 20
1 3 20

stdout

6

Example 2

stdin

4 5
0 1 5
0 2 10
1 2 10
2 3 10
1 3 5

stdout

-1

Output

You need to write a single line with an integer: the minimum amount of money you need to spend so that the new shortest path between city $0$ and city $N-1$ always passes through a new city. If it is not possible to achieve this, you need to write $-1$.

Notes

In the first sample case, it is possible to upgrade the railway between cities $2$ and $3$ so that the new shortest path passes through city $2$.




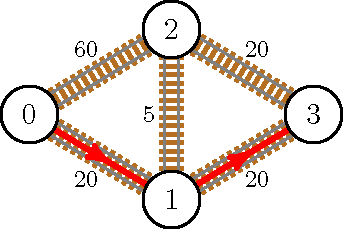
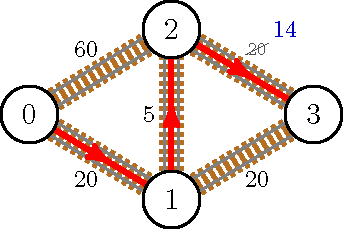
In the second sample case, it is not possible to upgrade a railway so that the new shortest path passes through a new city.