- Lina, acum au apărut dungi verzi pe monitor, cred că s-a stricat placa grafică.
- Aoleu, Vasile!
- Cred că e de la aghiasma pe care am turnat-o pe laptop.
- Ah, deci aghiasma a fost mai „eficientă” decât ne-am așteptat!
-- Vasile cu Lina, După un botez eșuat
Ana și Bob se plictisesc în vacanță. Au găsit în orașul pe care îl vizitează o revistă cu multiple jocuri. Următorul le-a sărit la ochi:
Jocul se joacă cu un arbore înrădăcinat (consultați pagina a treia pentru mai multe detalii). Se va plasa un unic pion în rădăcină. Jocul se joacă în mai multe ture, fiecare luând aceiași pași. Anume, într-o tură:
- Primul Jucător alege cel mult o muchie din arbore și o blochează permanent (poate și să nu facă nimic).
- Apoi, Al Doilea Jucător trebuie să mute pionul într-un fiu. Dacă toate muchiile spre fii sunt blocate, jocul se termină. Altfel, alege un fiu spre care muchia este neblocat și mută pionul în acel fiu.
Scorul jocului va fi la distanța față de rădăcină a pionului când se termină jocul. Primul Jucător trebuie să își facă mutările astfel încât scorul final să fie minim posibil, iar Al Doilea Jucător trebuie să le facă încât scorul final să fie maxim posibil. Astfel, scopul Primului Jucător este ca pionul să ajungă cât mai aproape de rădăcină, pe când Al Doilea Jucător încearcă să îl facă să ajungă cât mai departe de aceasta.
Ana va lua rolul de Primul Jucător, iar Bob rolul de Al Doilea Jucător. Ana și Bob au parcurs un drum plin de provocări și eforturi pentru a atinge acest punct culminant în ascensiunea lor ca logicieni. Astfel, puteți să considerați că fiecare joacă fiecare joc în mod perfect optim pentru a-și atinge obiectivul.
După câteva ture, copiii vor să facă jocul mai interesant. Astfel, își vor genera un arbore infinit pe care să se joace. Acesta este generat prin următorul proces:
- Inițial, un nod rădăcină de valoare asociată 1 este creat.
- Apoi, mereu când un nod de valoare apare, i se vor atașa ca fii noduri de valori asociate , . Acestea, la rândul lor, vor genera noi noduri, și tot așa. Amintim că indicii nodurilor nou create pot fi aleși arbitrar, singura precizare a acestui procedeu privește valorile asociate.
Cerință
Ana are ranchiună pe Bob de ceva vreme, așa că pentru a-i face o mică farsă, vrea să-l convingă că este o clarvăzătoare. Astfel, ea îți va da configurația unui joc pe care îl vor juca, și vrea să-i spui dinainte care va fi scorul jocului la finalul mutărilor. Ea observă că există cazuri în care jocul va merge la infinit, caz în care doar trebuie să-i comunici .
Date de intrare
Pe prima linie se va citi , numărul de valori existente pe care le pot avea nodurile.
Pe a -a din următoarele linii se va afla mai întâi , apoi valori , , \dots, .
Date de ieșire
Se va afișa o singură valoare: dacă jocul merge la infinit, sau scorul lui Bob la finalul lui altfel.
Restricții și precizări
- ;
- , și în particular , unde cu s-a notat suma tuturor -urilor prezente într-un test.;
- .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 6 | |
| 2 | 25 | și |
| 3 | 22 | |
| 3 | 21 | și |
| 4 | 26 | Fără restricții suplimentare. |
Exemplul 1
stdin
3
2 2 3
1 1
2 3 3
stdout
1
Exemplul 2
stdin
4
2 1 2
3 1 3 4
2 2 3
1 1
stdout
-1
Explicație
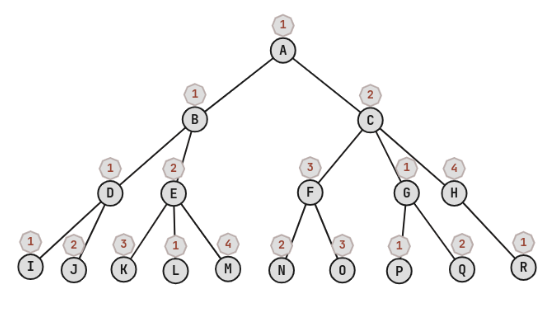
Primele 4 nivele ale arborelui infinit descris de al doilea exemplu. Valorile adiacente nodurilor reprezinta valorile asociate acestora atribuite conform procedeului. Notăm că arborele continuă în mod infinit din acest punct.
Arbore înrădăcinat
Un arbore înrădăcinat este un grup de puncte (numite formal, noduri) conectate între ele prin linii (numite formal, muchii), asemănător cu un copac, unde un punct special este considerat începutul sau „rădăcina”. Această grupare de linii și puncte respectă următoarele condiții:
- Fiecare punct este conectat direct sau indirect la „rădăcină”, aceasta fiind desenată ca nodul cel mai sus.
- Liniile nu formează bucle sau cercuri — poți merge de la un punct la altul printr-o singură succesiune de linii.
- Considerând succesiunea de puncte și linii ce conectează rădăcina de vreun alt punct , numim părinte ultimul punct parcurs în acest drum înainte de . De asemenea, numim fii unui nod mulțimea punctelor care îl au ca părinte pe .
- Vă puteți imagina că începeți de la rădăcină și „cresc” (în jos) punctele pe ramuri, fără să se întoarcă înapoi.
În desenul dat, rădăcina este . Pentru nodul , părintele său este , iar fii săi sunt și .