Banii mulți se fac ușor, banii puțini se fac greu.
--- 'Claus
Vasile este prietenul Linei. Recent, Vasile și-a făcut un cont de Pinance pentru a petrece mai mult timp investind în criptomonede decât la biserică. Surpriza lui a venit într-o zi când, fără vreun motiv aparent, a observat că investițiile lui au dat roade. Surprins de acest eveniment, a decis să analizeze evenimentele ce au avut loc în Plockchain care l-au adus la aceste culmi. Vasile ne-a explicat că ne putem imagina că Plockchain-ul funcționează în felul următor:
La început, în sistem există cereri de tranzacții, indexate de la la , a -a din ele având un comision la efectuare de și o unică altă cerere de care este direct dependentă . Se spune că cererea cu indexul era primordială sistemului și nu are nicio dependență. Vasile a observat mișcările din Plockchain și le-a clasificat în trei tipuri:
- Apare o nouă cerere cu comision inițial , a cărei dependență directă este . Indexul acestei cereri va fi , unde este numărul de cereri adăugate anterior prin acest procedeu. Astfel, prima cerere adăugată are indexul .
- Este modificat comisionul unei cereri cu index din în .
- Este ștearsă complet din registru cererea cu index . Se garantează că nu există o altă cerere astfel încât (nu depindea nicio cerere de ).
Lina, uimită de explicațiile lui Vasile, a început să se întrebe adesea de-a lungul acestor modificări următoarea întrebare:
Considerând toate cererile care există acum în sistem, cu ce comision ar fi răsplătit un hacker dacă ar efectua toate cererile care se află la cel mult dependențe în jos față de o cerere ?
Spunem că o cerere se află la cel mult dependențe în jos față de dacă și numai dacă și , sau și se află la cel mult dependențe în jos față de . Considerăm de asemenea că, în urma efectuării unor cereri, hackerul primește suma comisioanelor aferente cererilor. Desigur, întrebările Linei nu au niciun efect asupra sistemului, acesta rămânând la fel în urma acestei operații. Din vina sistemului robust al Plockchain-ului, este același în orice întrebare de-a Linei.
Cerință
Vasile știe că ziua Linei va fi curând, așa că s-a gândit să-i ofere cel mai bun cadou din lume: O listă de numere ce reprezintă răspunsurile la întrebările ei. Cu toate acestea, el este mult prea ocupat să o facă singur, așa că te-a delegat pe tine să le afli.
Date de intrare
Pe primul rând se află numerele , și , reprezentând numărul de cereri din sistemul original, numărul de modificări explicate de Vasile sau întrebări de-ale Linei, și constanta din întrebările Linei.
Urmează pe al doilea rând numere, al -lea reprezentând , comisionul inițial al cererii cu indexul .
Urmează pe al treilea rând numere, al -lea reprezentând , cererea de care este direct dependentă cererea cu indexul .
Urmează apoi rânduri, primul număr de pe fiecare fiind , reprezentând tipul operației. Apoi:
- Dacă , urmează și , reprezentând parametrii cererii nou apărute.
- Dacă , urmează și , reprezentând indexul cererii a cărei comision se modifică respectiv valoarea în care se modifică.
- Dacă , urmează , reprezentând indexul cererii care este acum ștearsă din sistem.
- Dacă , urmează , reprezentând indexul cererii pentru care pune Lina întrebarea.
Date de ieșire
În urma fiecărei întrebări (operație cu ), se va afișa un singur număr, anume răspunsul la întrebarea Linei pentru sistemul curent.
Restricții și precizări
- ;
- ;
- ;
- pentru toate operațiile.
- pentru toate operațiile de tipul , unde cu am notat indexul cererii nou adăugate în urma operației.
- și , pentru orice cerere inițială .
- Se garantează că pentru orice operație cererile implicate in aceasta există la momentul efectuării operației.
- Se garantează că nicio operație de tipul va fi efectuată asupra cererii cu numărul .
- Se garantează că nicio operație de tipul va fi efectuată asupra unei cereri pentru care există la momentul efectuării un astfel încât .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 13 | |
| 2 | 11 | , pentru , iar pentru orice operație |
| 3 | 16 | pentru orice operație |
| 4 | 10 | |
| 5 | 14 | , pentru , iar sau pentru orice operație |
| 6 | 10 | , pentru , iar sau pentru orice operație |
| 7 | 26 | Fără restricții suplimentare. |
Exemplu
stdin
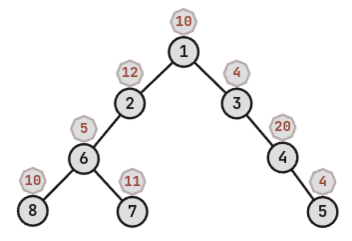
8 7 2
10 12 4 20 4 5 11 10
1 1 3 4 2 6 6
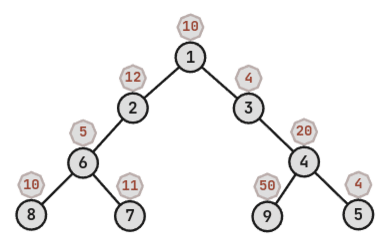
1 50 4
4 3
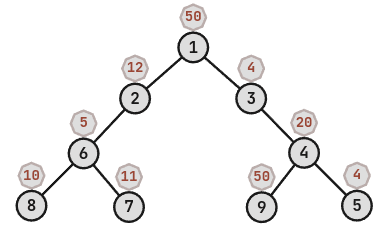
2 1 50
4 1
2 6 35
1 5 7
4 6
stdout
78
91
61
Explicație
Pentru prima interogare, cererile care sunt la dependențe în jos față de cererea sunt , , , cu costurile , , , . Astfel, trebuie să afișăm .