În timp ce făcea curat în Muzeul de Artă Modernă, Henry a găsit o sculptură formată din $N$ bile numerotate cu numere naturale distincte de la $1$ la $N$, ataşate între ele prin $N-1$ bare. Perspicace, Henry a realizat că sculptura reprezintă un arbore binar care are următoarele proprietăţi:

1. Cu excepția bilei aflate în vârful sculpturii (care este ataşată de tavan), fiecare bilă $X$ este ataşată printr-o bară de o altă bilă $P$ aflată deasupra ei. Astfel, vom spune că $P$ este părintele lui $X$.
2. Fiecare bilă poate avea maxim $2$ bile care se ataşează sub ea: opțional una spre stânga (fiul stâng) şi opțional una spre dreapta (fiul drept).
3. Dacă o bilă este numerotată cu un număr natural $X$, atunci toate bilele care sunt ataşate de ea, direct sau indirect prin bara dinspre stânga (subarborele stâng) sunt numerotate cu valori mai mici decât $X$, iar toate bilelele ataşate de ea, direct sau indirect prin bara dinspre dreapta (subarborele drept) sunt numerotate cu valori mai mari decât $X$.

Ca parte a noilor facilităţi interactive ale muzeului, lângă sculptură se află o machetă mobilă a acesteia, formată tot din $N$ bile numerotate de la $1$ la $N$, ataşate între ele prin $N-1$ bare. Deşi bilele ce formează macheta sunt conectate diferit, aceasta respectă aceleaşi reguli ($1$, $2$ și $3$) ca şi sculptura.

Deoarece a terminat curăţenia, Henry se gândeşte acum să modifice unele conexiuni din machetă, astfel încât aceasta să aibă aceeaşi formă ca şi sculptura (cu alte cuvinte, pentru fiecare $X$, $1 ≤ X ≤ N$, fiecare bilă numerotată cu $X$ din machetă să fie conectată cu bile având exact aceleași numerotări ca ale bilelor conectate cu bila $X$ din sculptură). Ca să facă lucrurile mai interesante, Henry se gândeşte să folosească doar două operaţii pentru a reaşeza macheta:

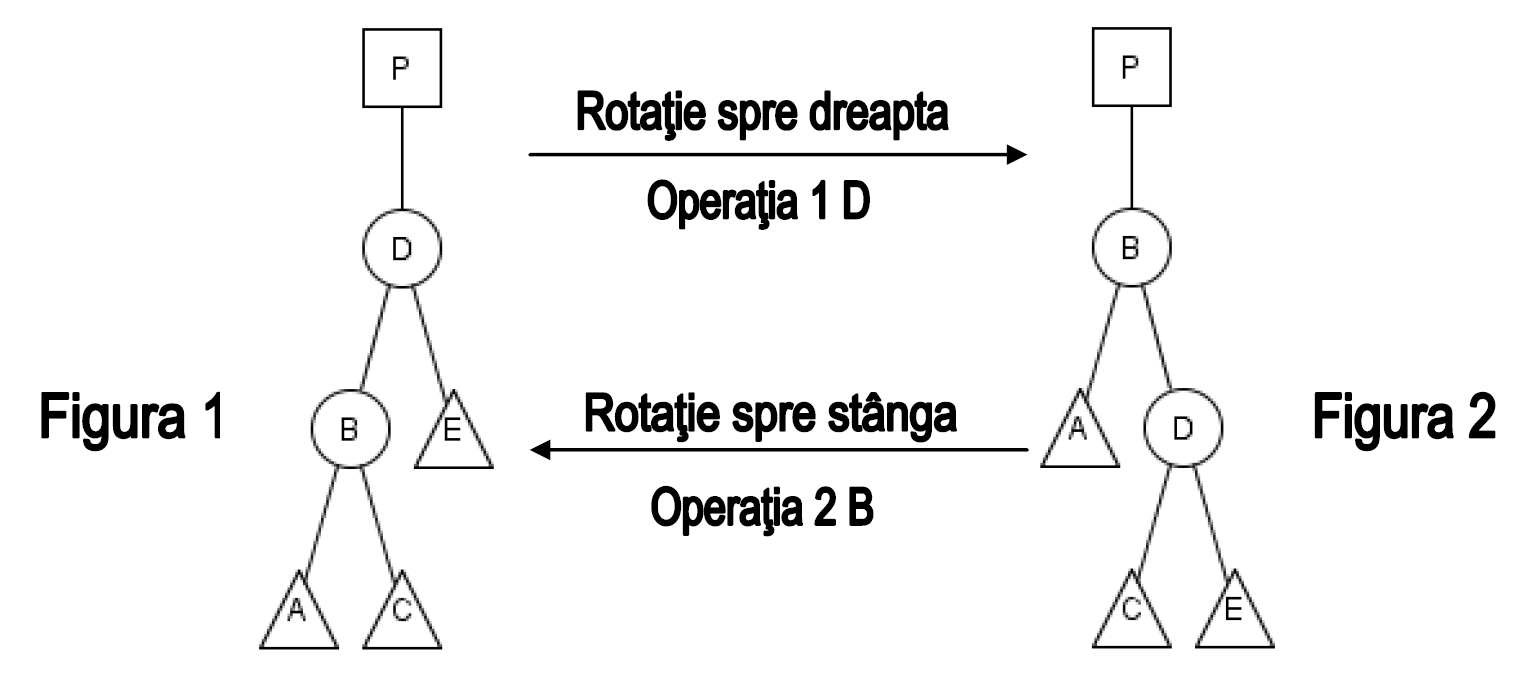
1. Rotaţia spre dreapta în jurul bilei numerotate cu $D$: pentru două bile $B$ și $D$, părintele $P$ (care poate exista sau nu) al bilei $D$ şi subarborii $A$, $C$ și $E$ (care pot exista sau nu) conectaţi ca în figura 1, se refac legăturile astfel încât $P, A, B, C, D$ şi $E$ să fie conectaţi ca în figura 2.
2. Rotaţia spre stânga în jurul bilei numerotate cu $B$: pentru două bile $B$ și $D$, părintele $P$ (care poate exista sau nu) al bilei $B$ şi subarborii $A$, $C$ și $E$ (care pot exista sau nu) conectaţi ca în figura 2, se refac legăturile astfel încât $P, A, B, C, D$ şi $E$ să fie conectaţi ca în figura 1.

Pentru orice tip de rotaţie, toate celelalte legături între bilele machetei rămân neschimbate. La o privire atentă, se observă că după orice operaţie de rotaţie, macheta respectă în continuare regulile $1$, $2$ şi $3$.

Deoarece Henry nu se pricepe cu adevărat decât la curăţenie, vă roagă pe voi să găsiţi o serie de rotaţii care aduc macheta la aceeaşi formă ca şi sculptura.

Date de intrare

Pe prima linie a fișierului de intrare rotatii.in se va găsi un număr natural $N$, reprezentând numărul de bile ce compun sculptura. Pe următoarele $N$ linii se va găsi descrierea machetei. Astfel, pentru fiecare $i$, $1 ≤ i ≤ N$, pe linia $1 + i$ se vor găsi câte două numere naturale separate printr-un spațiu $ML[i]$, $MR[i]$, reprezentând fiul stâng, respectiv fiul drept al bilei etichetate cu $i$ din machetă ($ML[i]$ și/sau $MR[i]$ pot fi $0$ în cazul în care bila $i$ nu are fiul corespunzător). În mod similar cu descrierea machetei, pe următoarele $N$ linii se va găsi descrierea sculpturii. Astfel, pentru fiecare $i$, $1 ≤ i ≤ N$, pe linia $1 + N + i$ se vor găsi câte două numere naturale separate printr-un spațiu $SL[i], SR[i]$, reprezentând fiul stâng, respectiv fiul drept al bilei etichetată cu $i$ din sculptură ($SL[i]$ și/sau $SR[i]$ pot fi $0$ în cazul în care bila $i$ nu are fiul corespunzător).

Date de ieșire

Pe prima linie a fișierului de ieșire rotatii.out se va afișa un număr $K$, reprezentând numărul de rotații necesare pentru a aduce macheta la aceeași formă ca și sculptura. Pe următoarele $K$ linii se vor afișa, în ordine, operațiile efectuate, sub forma:

• $1 \ D$, semnificând ca se efectuează o rotație spre dreapta în jurul bilei $D$ din machetă (vezi figura);
• $2 \ B$, semnificând ca se efectuează o rotație spre stânga în jurul bilei $B$ din machetă (vezi figura).

Între $1$ şi $D$, respectiv $2$ şi $B$ se va afla afişa exact un spaţiu.

Restricții și precizări

• $1 ≤ N ≤ 1 \ 000 \ 000$
• $K$ nu trebuie neaparat să fie minim.
• Pentru $50$ din teste, $1 ≤ N ≤ 2 \ 000$
• Se vor acorda $70$ din punctele pentru un test dacă operațiile afișate în fișierul de ieșire aduc macheta la forma sculpturii, iar programul rulează în limitele de timp și memorie indicate, dar $K > 2 \cdot N$.
• Se vor acorda $100$ din punctele pentru un test dacă, în plus, $K ≤ 2 \cdot N$.

Exemplu

rotatii.in

5
0 0
1 3
0 0
2 5
0 0
0 0
1 5
0 0
3 0
4 0

rotatii.out

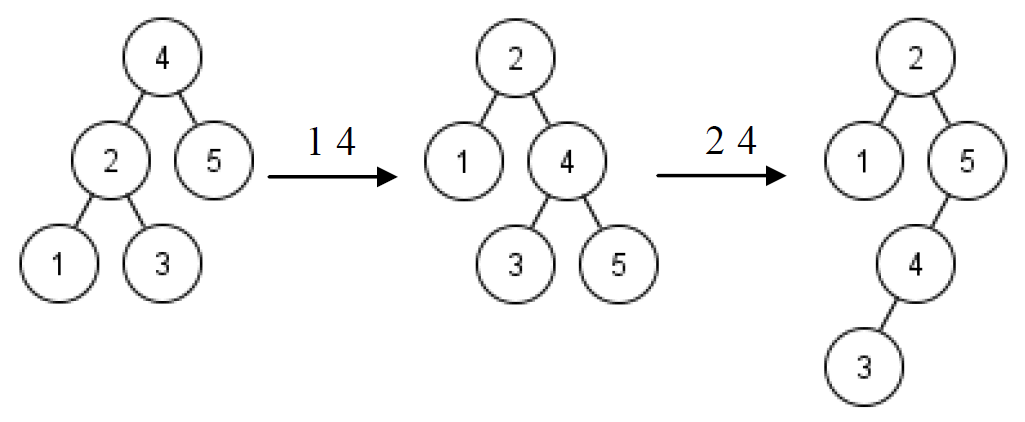
2
1 4
2 4

Explicații

Se va efectua întâi o rotaţie spre dreapta în jurul lui $4$, apoi o rotaţie spre stânga în jurul lui $4$, după cum se poate vedea în figură