Nika este o fetiță curioasă din fire. Ea a găsit în cutiuța bunicii un graf neorientat conex cu N noduri și N muchii, dintre care una singură este desemnată ca fiind muchia care închide un ciclu. Cunoscând faptul că fiecare muchie are un cost, Nika vă pune trei tipuri de întrebări:

• 0 a b : „Care este distanța minimă dintre nodurile a și b, dacă o muchie se poate parcurge cel mult odată?”
• 1 m c : „Cum arată graful dacă se modifică costul muchiei m la valoarea c?”. Graful se modifică prin aceasta operație, iar modificarea este persistentă.
• 2 a b c : „Cum arată graful dacă se șterge muchia care închide un ciclu, şi se pune muchie între a şi b de cost c?”. Graful se modifică prin această operație, iar noua muchie va deveni muchia care închide un ciclu. Modificarea este persistentă.

Din acest moment, scopul principal al vieții voastre a devenit rezolvarea problemei, pentru a intra în Lotul Național de Informatică.

Cerinţă

Răspundeți la întrebările puse de Nika cât mai repede (altfel sevaplictisișivețirămânefărăpremiu).

Date de intrare

Fişierul de intrare nikagraf.in conţine următoarele date:

• pe prima linie se vor afla două numere naturale N și Q reprezentând numărul de noduri ale grafului și numărul de întrebări ale fetiței;
• pe următoarele N linii se vor găsi câte trei numere x y c reprezentând muchia de la x la y de cost c. Primele N – 1 muchii definesc un arbore, iar ultima muchie va reprezenta muchia care închide un ciclu. Această muchie va fi schimbată în momentul în care se aplică o operație de tip 2.
• pe următoarele Q linii se vor găsi întrebările în formatul descris în enunț.

Date de ieşire

Fisierul de ieșire nikagraf.out va conține răspunsurile doar la întrebările de tip 0 (pentru celelalte vă crede pe cuvânt).

Restricţii şi precizări

• 1 ≤ N ≤ 100 000;
• 1 ≤ Q ≤ 200 000;
• $-2 \cdot 10^4 ≤ cost ≤ 2 \cdot 10^4$;
• Muchiile sunt indexate de la 1;
• Nu există muchie de la un nod la el însuşi şi nu există mai mult de o muchie între două noduri;
• Pentru 20% din teste N şi Q nu vor depăşi 3000;
• Pentru 30% din teste nu vor exista operaţii de tipul 1, iar pentru alte 30% din teste nu vor exista operaţii de tipul 2.
• Distanţa minimă între două noduri a şi b se defineşte ca suma costurilor muchiilor unui drum de lungime minimă între cele două noduri.

Exemple

nikagraf.in

4 5
1 2 2
1 3 1
2 4 1
2 3 1
0 4 1
1 1 1
0 4 1
2 4 3 0
0 4 1

nikagraf.out

3
2
1

Explicaţie

Graful iniţial este:

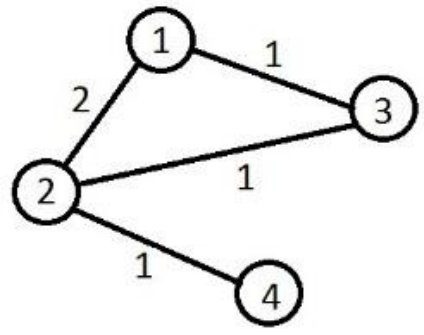
Se observă că distanţa de la 4 la 1 este 3 atât pentru drumul 4 – 2 – 1 cât şi pentru drumul 4 – 2 – 3 – 1.
Pentru a doua întrebare răspunsul este 2, mergând pe drumul 4 – 2 – 1.
Pentru a treia întrebare răspunsul este 1, mergând pe drumul 4 – 3 – 1.