Gigel este un pasionat al ordinii. Când se duce în vizită la bunica, întotdeauna face ordine în dulapul de bucătărie al bunicii, unde farfuriile stau în teancuri verticale, fără să fie, uneori, aranjate după mărimea lor. Ieri, când a vizitat-o pe bunica, s-a hotărât să aranjeze toate farfuriile într-un singur teanc, ordonate descrescător de la bază spre vârf, după diametru. Și pentru a da și o nuanță de joc acestei activități, s-a hotărât, că la fiecare mișcare va lua doar o farfurie din vârful unui teanc și va așeza în vârful unui alt teanc, și niciodată nu va pune o farfurie mai mare peste o farfurie mai mică.
Pentru a putea codifica mutările, cele trei teancuri de farfurii le vom denumi coloane și le vom numerota cu , și . În orice moment, pe oricare dintre coloane pot exista sau nu farfurii. Dacă o coloană nu conține nicio farfurie, vom spune că este goală. Pe o coloană goală se poate pune orice farfurie ce poate fi accesată. Dacă o coloană conține cel puțin o farfurie, atunci în vârful acestei coloane se va putea așeza o nouă farfurie numai dacă diametrul noii farfurii este mai mic sau egal cu diametrul farfuriei din vârful coloanei.
Rezolvarea problemei va consta dintr-o succesiune de operații. O operație constă în extragerea unei farfurii de pe o coloană și plasarea acesteia pe o altă coloană , respectând restricțiile de mai sus. Dată fiind o coloană , spunem că succesiunea de operații este corectă dacă, după executarea tuturor operațiilor, toate farfuriile se vor afla pe coloana , în ordinea descrescătoare a diametrelor de la bază spre vârf.
Cerință
Cunoscând configurația celor trei teancuri inițiale de farfurii, precum și numărul al coloanei pe care trebuie să se afle la final farfuriile, scrieți un program care să determine o succesiune corectă de operații.
Date de intrare
Fişierul de intrare farfurii.in conține linii. Pe linia se află numărul natural , ce reprezintă numărul de farfurii din coloana , urmat de numere naturale separate prin câte un spaţiu, reprezentând dimensiunile diametrelor farfuriilor de pe coloana de la bază spre vârf (dacă , atunci nu există farfurii pe coloana ). Pe ultima linie se află numărul , sau , reprezentând coloana pe care vor fi plasate toate farfuriile în final.
Date de ieșire
Fişierul de ieşire farfurii.out va conţine operațiile, în ordinea efectuării lor, câte o operație pe o linie. O operație va fi descrisă prin două numere separate prin spațiu cu semnificaţia: „farfuria din vârful coloanei se mută la vârful coloanei ”. Pe ultima linie se vor scrie numerele , separate prin spațiu.
Restricții și precizări
- dimensiunile diametrelor farfuriilor
- Soluția nu este unică. Se acceptă orice soluție corectă. Nu se cere optimizarea numărului de operații, dar rezolvarea problemei trebuie să se încadreze în timpul de execuție specificat
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 4 | Toate farfuriile sunt de aceeași dimensiune. |
| 2 | 11 | Există doar două dimensiuni diferite de farfurii. |
| 3 | 12 | Există doar trei dimensiuni diferite de farfurii. |
| 4 | 22 | Toate farfuriile sunt ordonate pe o singură coloană. |
| 5 | 14 | Toate farfuriile formează două coloane crescătoare de la bază spre vârf. |
| 6 | 18 | Toate farfuriile au dimensiuni diferite. |
| 7 | 19 | Fără restricții suplimentare |
Exemplu
farfurii.in
2 1 7
3 5 1 9
0
3
farfurii.out
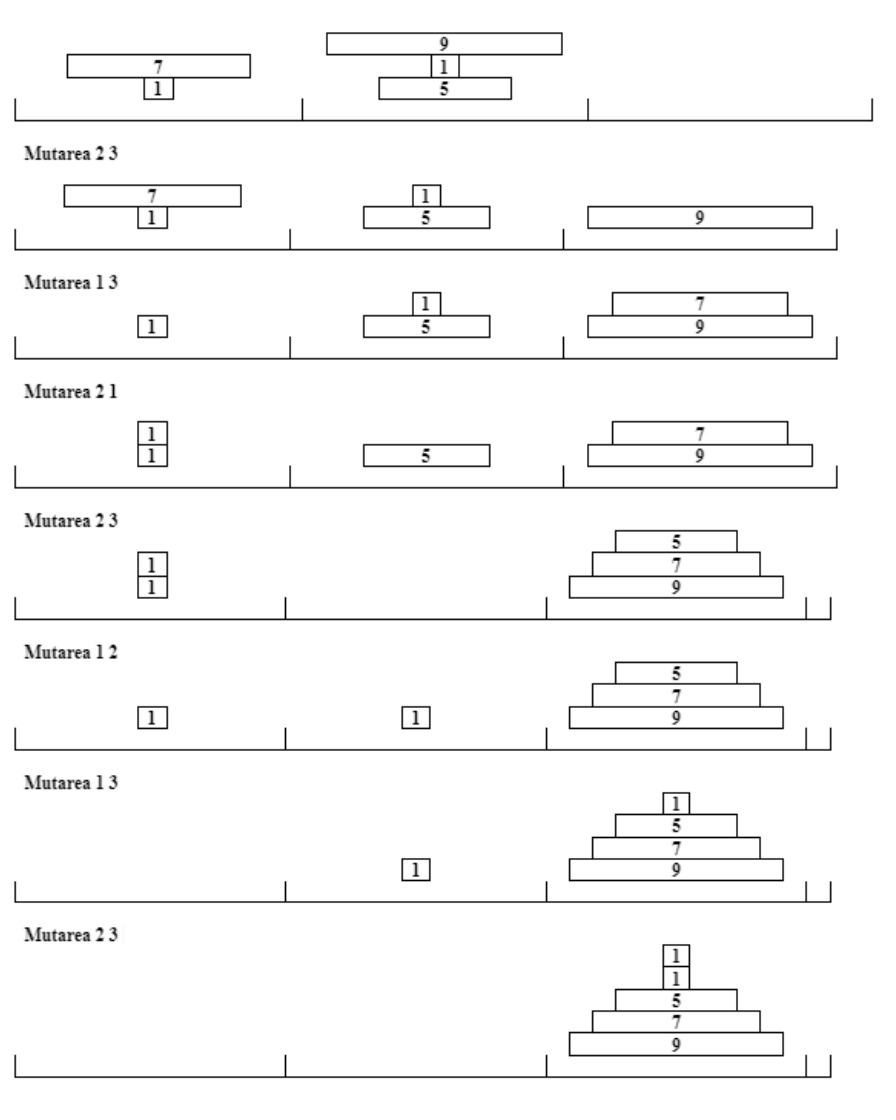
2 3
1 3
2 1
2 3
1 2
1 3
2 3
0 0
Explicație
Farfuriile trebuie să fie plasate pe coloana . Configurația inițială: