Donjon

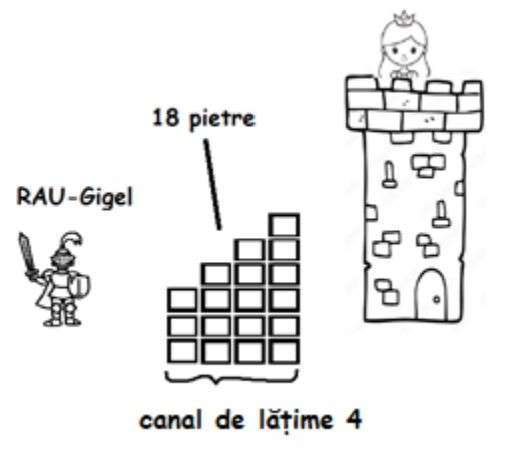
Căpcăunul cel rău o ține captivă pe frumoasa prințesă într-un castel izolat, într-un turn înalt. RAU-Gigel prinde de veste și se duce într-un suflet să o salveze. El trebuie să treacă un canal de apărare de lungime $K$, așezând $N$ pietre de dimensiuni egale cu unitatea, în formă de trepte de înălțimi $h$, $h+1$, $h+2$, $h+3$, ..., $h+K-1$. Prima treaptă trebuie să aibă cel puțin o piatră, iar dacă o singură piatră rămâne nedistribuită, toată construcția se face una cu pământul.

Dacă se cunosc: numărul $N$ de pietre magice și distanța $K$ dintre poziția lui RAU-Gigel și donjonul prințesei, putem să aflăm dacă RAU-Gigel va reuși să construiască treptele?

RAU-Gigel își încearcă șansele. Un eșec va însemna renunțarea la prințesă. O reușită însă, va conduce la o surpriză din partea căpcăunului, acesta îl va supune pe RAU-Gigel la o nouă provocare:

RAU-Gigel, flăcăul meu,
Te voi provoca la greu!
De testu’-l vei câștiga,
Pe prințesă vei avea!

Și îi propune următorul test: „vom alege, pe rând, câte o treaptă dintre cele construite de tine și vom dărâma din ea oricâte pietre, minim una, cel mult toate. Prea-frumoasa prințesă va rămâne cu acela dintre noi, care va dărâma și ultima piatră”. RAU-Gigel va începe primul, iar atât RAU-Gigel cât și căpcăunul vor juca responsabil, adică vor face întotdeauna alegerea cea mai bună în interesul propriu. Reușește RAU-Gigel să elibereze prințesa?

De exemplu, daca avem $N = 5$ și $K = 2$, RAU-Gigel construiește $2$ trepte de înălțimi $2$ și $3$, astfel nu rămân pietre nefolosite. Să vedem acum cine va câștiga cea de-a doua provocare. RAU-Gigel va alege primul. El poate alege prima treaptă și poate dărâma toate pietrele de pe ea, însă aceasta va fi o alegere greșita, întrucât căpcăunul va dărâma la rândul lui toate pietrele de pe treapta a doua, păstrând prințesa captivă. Așadar, RAU-Gigel nu va începe prin a dărâma toate pietrele de pe o treaptă.

O altă variantă ar fi ca RAU-Gigel să aleagă prima treaptă, de unde să dărâme o singură piatră. Aceasta iarăși ar fi o mutare greșită, căpcăunul ar dărâma la rândul său două pietre de pe treapta a doua, iar acum, orice alegere ar face RAU-Gigel, ar pierde.

Cu siguranță, RAU-Gigel va alege treapta a doua de unde va dărâma o singură piatră. Căpcăunul nu va avea ieșire din această situație: dacă dărâmă ambele pietre de pe oricare treaptă, RAU-Gigel le va dărâma pe celelalte două și va câștiga, dacă căpcăunul dărâmă numai o piatră de pe oricare treaptă, RAU-Gigel va alege o piatră de pe cealaltă treaptă, apoi din nou, va lua fiecare câte o piatră, și căpcăunul nu va mai avea ce dărâma, iar RAU-Gigel va pleca cu prea frumoasa fată.

Cerință

Se vor testa mai multe scenarii de tipul celui de mai sus.

Date de intrare

Fișierul de intrare donjon.in conține pe prima linie numărul $Q$ reprezentând numărul de scenarii, apoi pe următoarele $Q$ rânduri se vor afla câte două numere $N$ și $K$ separate cu un spațiu, cu semnificația din enunț.

Date de ieșire

Fișierul donjon.out va conține $Q$ rânduri pe care se află răspunsurile la cele $Q$ scenarii, astfel: dacă RAU-Gigel nu reușește să construiască treptele, se va răspunde cu litera mare C. Dacă reușește să construiască treptele, se va răspunde cu $x \ y$, separate printr-un spațiu, unde $x$ este litera mare C dacă căpcăunul câștigă proba a doua, respectiv litera mare G dacă RAU-Gigel salvează prințesa, iar $y$ este un număr natural nenul reprezentând numărul de pietre folosite de RAU-Gigel pentru prima treaptă.

Restricții și precizări

• $1 \leq Q \leq 10$
• $2 \leq N \leq 10^{18}$
• $2 \leq K \leq 10^9$
• Pentru teste în valoare de 20 de puncte: $Q \leq 5$, $N \leq 10$ pentru toate scenariile.
• Teste în valoare de 30 de puncte sunt favorabile lui RAU-Gigel pentru toate scenariile, în sensul că, dacă acesta trece de prima provocare și reușește să construiască treptele conform cerinței, atunci se garantează că va câștiga și cea de-a doua provocare.

Exemplu

donjon.in

3
5 2
6 3
5 3

donjon.out

G 2
C 1
C

Explicație

Avem $3$ scenarii.

În primul scenariu sunt $5$ pietre, iar lățimea canalului este $2$. Răspunsul pentru acest scenariu va fi G 2 pentru că RAU-Gigel reușește la ambele provocări, iar prima treaptă construită are $2$ pietre (vezi explicația mai sus).

Pentru scenariul al doilea, avem $N = 6$ și $K = 3$. RAU-Gigel trece de prima proba și construiește cele $3$ trepte: $1$, $2$, $3$. Dar, oricum ar încerca să le dărâme, căpcăunul va avea ultima aruncare. Răspunsul pentru acest scenariu va fi C 1 pentru că, deși RAU-Gigel trece de prima provocare așezând o piatră ca primă treaptă, el pierde jocul final.

Pentru ultimul scenariu, răspunsul este C, RAU-Gigel nu poate construi $3$ trepte cu $5$ pietre, conform cerinței, care să îi asigure trecerea către donjonul prințesei.