Zid

Fascinată de cultura chineză și Marele Zid Chinezesc, Andra s-a hotărât să își construiască propriul zid în miniatură, de înălțime $N$ și lățime $M$ , din piese roșii și galbene pe care le deține.

Ea are la dispoziție un număr nelimitat de piese cu lățimea de o unitate și toate înălțimile posibile. Piesele roșii (hóng) au înălțimea impară $(1, 3, 5, \dots)$, pe când piesele galbene (huáng) au înălțimea pară $(2, 4, 6, \dots)$. Piesele nu pot fi rotite și pot fi plasate doar pe verticală.

Deoarece culoarea galbenă este considerată cea mai prestigioasă în cultura chineză, Andra vrea ca suma lungimilor tuturor pieselor galbene ce alcătuiesc zidul să fie egală cu un număr $K$, special ales astfel încât să aducă noroc. Mai mult de atât, ea se întreabă în câte moduri poate construi zidul astfel încât această condiție să fie respectată. Întrucât această cerință “pare chineză” pentru ea (chiar dacă este vorbitoare de limba chineză!), a decis să vă ceară ajutorul, auzind că vă simțiți norocoși în anul dragonului.

Întrucât această cerință “pare chineză” pentru ea (chiar dacă este vorbitoare de limba chineză!), a decis să vă ceară ajutorul, auzind că vă simțiți norocoși în anul dragonului.

Cerință

Date fiind $N, M$ și $K$, determinați numărul de moduri de a construi zidul în condițiile date.

Date de intrare

Singura linie a fișierului de intrare zid.out conține valorile $N$, $M$ și $K$, cu semnificația din enunț.

Date de ieșire

Singura linie a fișierului de ieșire zid.out va conține numărul de moduri de a construi zidul modulo $10^9 + 7$.

Restricții și precizări

• $1 \leq N, M \leq 5 \ 000$
• $0 \leq K \leq N$
• Două modalități de a construi zidul se consideră identice dacă sunt formate din aceleași tipuri de piese plasate în același mod. De exemplu, există două moduri de a construi un zid de $4 × 1$ complet galben.

Exemplul 1

zid.in

5 1 2

zid.out

6

Explicație

Toate cele $6$ configurații de ziduri cu înălțimea $5$, lățimea $1$ și $K = 2$ posibile sunt ilustrate în prima figură.

Exemplul 2

zid.in

2 2 2

zid.out

2

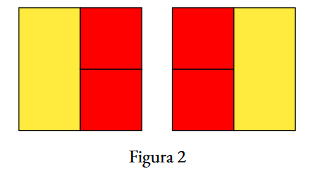
Explicație

Toate cele $2$ configurații sunt ilustrate în cea de a doua figură.