M and Ms

Andra are un pachet cu $n$ tipuri de buline de ciocolată, cu câte $c_i$ buline de fiecare tip $i$. Numărul $c_i$ depinde de patru factori, notați cu $x$, $y$, $z$, $t$, și se calculează astfel:

• $c_1 = x$
• $c_i = (c_{i−1} \cdot y)\ \%\ t + z$, $\forall i$, $2 \leq i \leq n$

unde s-a notat cu $a\ \%\ b$ restul împărțirii numărului natural $a$ la numărul natural nenul $b$.

Andra dorește să utilizeze toate bulinele pentru a construi piramide, fiecare fiind formată din unul sau mai multe rânduri, numerotate începând de la $1$. Pentru fiecare piramidă în parte, pe rândul $i$, se află $2^{i-1}$ buline. Spre exemplu, pe rândul $8$ al unei piramide, se află $2^7 = 128$ de buline de ciocolată. Pe fiecare rând al unei piramide se află unul sau mai multe tipuri de buline, iar același tip de buline se poate folosi pe oricâte rânduri. Dintre piramidele care se pot forma, cele serioase conțin pe fiecare rând doar un tip de buline.

Cerință

Folosind toate bulinele, ajutați-o pe Andra să determine:

1. Numărul minim de piramide de ciocolată pe care le poate forma.
2. Numărul minim de piramide serioase de ciocolată pe care le poate forma, astfel încât toate cele obținute să fie de acest fel.

Date de intrare

Fișierul de intrare mandms.in conține pe prima linie numărul $p$, care poate fi doar $1$ sau $2$.

Pe a doua linie a fișierului, se află numărul natural $n$, cu semnificația din enunț.

Pe a treia linie se află numerele naturale $x$, $y$, $z$, $t$, în această ordine, cu semnificația din enunț.

Date de ieșire

Dacă $p = 1$, fișierul de ieșire mandms.out conține un număr natural, reprezentând valoarea precizată la cerința 1.

Dacă $p = 2$, fișierul de ieșire mandms.out conține un număr natural, reprezentând valoarea precizată la cerința 2.

Restricții și precizări

• $1 \leq n \leq 2 \ 000 \ 000$
• $1 \leq x, y, t < 2^{64}$
• $0 \leq z < 2^{64}$
• $1 \leq c_i < 2^{64}$
• $0 \leq c_i \cdot y < 2^{64}$, $\forall i$, $2 \leq i \leq n$

Exemplul 1

mandms.in

1
8
3 15 18 17

mandms.out

5

Explicație

$x = 3$, $y = 15$, $z = 18$, $t = 17$

Numărul de buline de cele $8$ tipuri se calculează astfel:

• $c_1 = x = 3$
• $c_2 = (3 \cdot 15)\ \%\ 17 + 18 = 29$
• $c_3 = (29 \cdot 15)\ \%\ 17 + 18 = 28$
• $c_4 = (28 \cdot 15)\ \%\ 17 + 18 = 30$
• $c_5 = (30 \cdot 15)\ \%\ 17 + 18 = 26$
• $c_6 = (26 \cdot 15)\ \%\ 17 + 18 = 34$
• $c_7 = (34 \cdot 15)\ \%\ 17 + 18 = 18$
• $c_8 = (18 \cdot 15)\ \%\ 17 + 18 = 33$

Numărul minim de piramide care se pot forma este $5$.

O posibilă configurație a piramidei este următoarea:

În această configurație, avem o piramidă cu $7$ rânduri, una cu $6$ rânduri, una cu $3$ rânduri, una cu $2$ rânduri, și una cu un singur rând.

Exemplul 2

mandms.in

2
8
3 15 18 17

mandms.out

7

Explicație

$x = 3$, $y = 15$, $z = 18$, $t = 17$

Numărul de buline de cele $8$ tipuri se calculează astfel:

• $c_1 = x = 3$
• $c_2 = (3 \cdot 15)\ \%\ 17 + 18 = 29$
• $c_3 = (29 \cdot 15)\ \%\ 17 + 18 = 28$
• $c_4 = (28 \cdot 15)\ \%\ 17 + 18 = 30$
• $c_5 = (30 \cdot 15)\ \%\ 17 + 18 = 26$
• $c_6 = (26 \cdot 15)\ \%\ 17 + 18 = 34$
• $c_7 = (34 \cdot 15)\ \%\ 17 + 18 = 18$
• $c_8 = (18 \cdot 15)\ \%\ 17 + 18 = 33$

Numărul minim de piramide serioase care se pot forma, astfel încât toate cele obținute să fie serioase, este $7$.

O posibilă configurație a piramidei este următoarea:

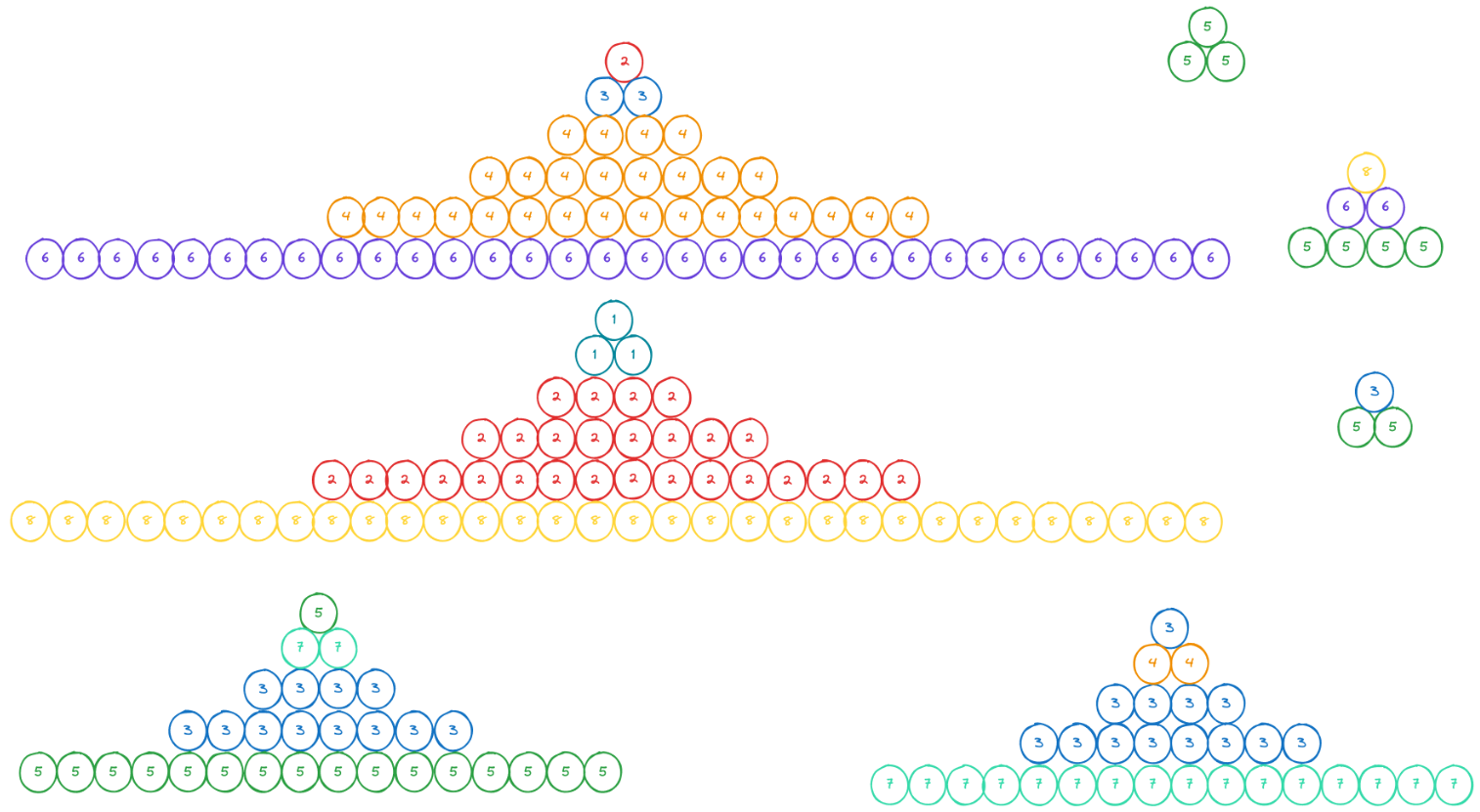
În această configurație, avem două piramide cu $6$ rânduri, două cu $5$ rânduri, una cu $3$ rânduri, și două cu $2$ rânduri.