Who doesn't love walks?
The map of Shumen can be represented as crossroads, numbered with the integers from to with bidirectional streets between them, numbered with the integers from to . Every street connects a pair of different crossroads, and there isn't a pair of crossroads that are connected by two different streets. One could get from any crossroad to any other by traversing through the given streets.
Kyushо and his dog Bobby were having a night walk right before yesterday's party. They traversed all the streets at least once in the walk. Bobby, the dog, is exceptionally intelligent but has problems memorizing the order of the traversed streets and that's why it memorized them rather chaotically and sometimes even contradictory. For example, it is possible that for some street the dog has memorized that is was traversed at moment but there is no street that was memorized being traversed at moment . Formally, Bobby, the dog, has memorized that the -th street between crossroads and was traversed at moment .
In the morning, Kyusho realized that he also has problems remembering last night and wanted to recall the traversed crossroads from the walk as best as possible. To do this, he will take another walk, starting from his hotel in crossroad . As he does not want to get lost, he will traverse the streets in a way, that every subsequently passed street has been traversed at a later moment than the previous one (according to the memories of Bobby, the dog), or in other words, > . It is possible to pass a crossroad more than once.
Task
Kyushо wants his new walk to contain as many streets as possible and end at some crossroad, but he still hasn't decided where he will stop. So, he desires to know the longest walk to every crossroad following the rules of moving from the previous paragraph. Please, help him by writing a program, which finds the inquired maximal lengths with regards to the number of passed streets.
Input data
The first line of the standard input contains the two integers and – the count of the crossroads and the count of the streets between them. Each of the rest lines contains three integers – , and , which describe a street between the crossroads with numbers and , traversed at moment (according to the memories of Bobby, the dog).
Output data
The only line of the standard output should contain integers, each separated by a space – the maximal lengths of walks from crossroad to all crossroads . If there is no possible walk to one of them, you should print as the maximal length of a walk to this crossroad.
Constraints and clarifications
- ,
| # | Score | Constraints |
|---|---|---|
| 1 | 0 | Example |
| 2 | 10 | , |
| 3 | 7 | |
| 4 | 29 | , |
| 5 | 27 | and for |
| 6 | 7 | |
| 7 | 14 | for |
| 8 | 6 | No additional constraints |
Example
stdin
8 12
1 4 9
1 6 4
1 5 1
3 4 11
3 5 10
5 6 2
6 2 6
2 8 7
5 8 8
7 8 5
5 7 14
3 7 12
stdout
3 3 6 7 8 2 7 4
Explanation
Illustration of the streets and crossroads:
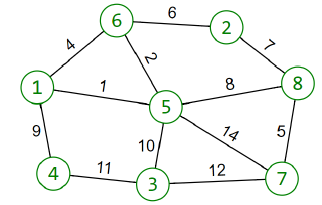
Optimal walk to crossroad with number is the following: .
Notice, that when we are at crossroad in the walk, we cannot continue to crossroad because the moment of that street is but we have come from a street with moment .