Marcel, a successful entrepreneur, owns a trucking company that operates transport services across the country. Facing resource allocation issues, he hired the firm "Ditches and Bridges" to analyze his transport network.
The experts modeled Marcel's network as a connected undirected graph with cities and direct roads. A direct road between two cities and is represented by an edge and has a length . Between other cities, the road is indirect, being a simple path in the graph. A path is called simple if the edges do not repeat.
With this model in mind, the following observation was made: some direct roads are more critical than others. A direct road is critical if its removal would make it impossible to deliver goods between two or more cities. Thus, the following notation was made: is the sum of the lengths of the critical roads on the direct or indirect route from city to city .
Task
The experts now need to evaluate the importance of these critical roads, and since the company makes deliveries between all pairs of cities, they need to calculate the following sum:
The sum can be very large, so Marcel will be satisfied with finding the remainder when divided by . As the young entrepreneur tends to make dubious financial decisions, you need to help the experts calculate this sum, as they are overwhelmed by the situation.
Input data
The first line contains and , the number of cities and the number of direct roads between the cities, respectively. Then follow lines with 3 values separated by a space: , , and , indicating that there is a direct road of length between cities and .
Output data
On the first line, output a single integer, the required sum modulo .
Constraints and clarifications
- ;
- ;
- , where is the length of a direct road.
| # | Points | Constraints |
|---|---|---|
| 0 | 0 | Examples |
| 1 | 6 | |
| 2 | 12 | and the network is a tree |
| 3 | 34 | The network is a tree |
| 4 | 48 | No additional constraints |
Example 1
stdin
7 7
1 4 2
6 3 3
3 1 3
3 5 5
2 3 4
5 6 5
1 7 3
stdout
90
Explanation
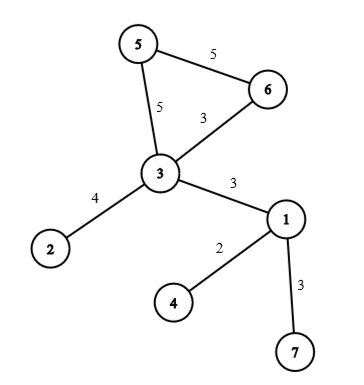
The sum includes contributions from:
In this example, because no road between these pairs has a critical edge.
Example 2
stdin
8 8
7 6 17
2 1 10
6 2 5
2 5 19
3 1 5
1 8 4
7 2 1
5 4 18
stdout
567