Tibi este un pasionat al matematicii, dar și un artist talentat. În timpul școlii, el a învățat să lucreze cu intervale de numere, pe care le reprezintă vizual pe ciorne cu ajutorul unor segmente colorate și stilizate în diferite moduri pentru o mai bună întelegere a problemei pe care o rezolvă. După ce și-a terminat temele la matematică, pe ciornele sale au rămas o mulțime de segmente de diferite tipuri, fiecare reprezentând un interval închis între numerele din problemele rezolvate. Într-o zi, s-a uitat la ciornele sale și s-a gândit la o problemă pe care vă invită să o rezolvați:

Cerință

Se dă un număr $n$ de segmente diferite. Fiecare segment $1 \leq i \leq n$ este definit de tipul său ($tip_i$), punctul de start ($st_i$) și punctul final ($dr_i$). Segmentul include toate punctele din intervalul $[st_i , dr_i]$, inclusiv, și îndeplinește condiția $tip_i \leq k$, unde $k$ este numărul total de tipuri diferite. Două segmente sunt considerate conectate dacă au cel puțin un punct comun și sunt de tipuri diferite. Ele fac parte din același grup dacă sunt conectate direct sau printr-o secvență de segmente conectate direct. Sarcina voastră este să determinați numărul de grupuri de segmente care se formează pe fiecare ciornă a lui Tibi.

Date de intrare

Fișierul de intrare segmente.in conține pe prima linie un număr natural $t$ reprezentând numărul de cazuri de testare (de ciorne). Fiecare are următoarea structură:

• Prima linie a unui caz de testare conține două numere întregi $n$ și $k$.
• Pe următoarele $n$ linii se va afla un triplet de forma ($tip_i, st_i, dr_i$), definind al $i$-lea segment din cazul de testare, unde $1 \leq i \leq n$.

Date de ieșire

Pentru fiecare dintre cazurile de testare, $t$, afișați în fișierul de ieșire segmente.out pe o linie separată numărul de grupuri pe care segmentele le formează în acel caz.

Restricții și precizări

• $1 \leq t \leq 1\ 000$
• $1 \leq n \leq 200\ 000$
• $1 \leq k \leq 1\ 000$
• $1 \leq tip_i \leq 1\ 000$ și $0 \leq st_i \leq dr_i \leq 10^9$ pentru orice $i$ de la $1$ la $n$.
• Este garantat că suma valorilor lui $n$ peste toate cazurile de testare (notăm cu $\sum{n}$) nu depășește $200\ 000$ (toate ciornele lui Tibi nu au mai mult de $200\ 000$ de secvențe).

Exemplu

segmente.in

3
6 3
1 2 5
2 4 9
1 7 12
1 11 15
3 14 18
3 17 20
4 4
1 1 4
3 2 7
4 5 7
2 8 10
7 2
2 3 8
1 13 13
1 1 4
2 5 7
1 8 11
1 10 13
2 12 14

segmente.out

3
2
3

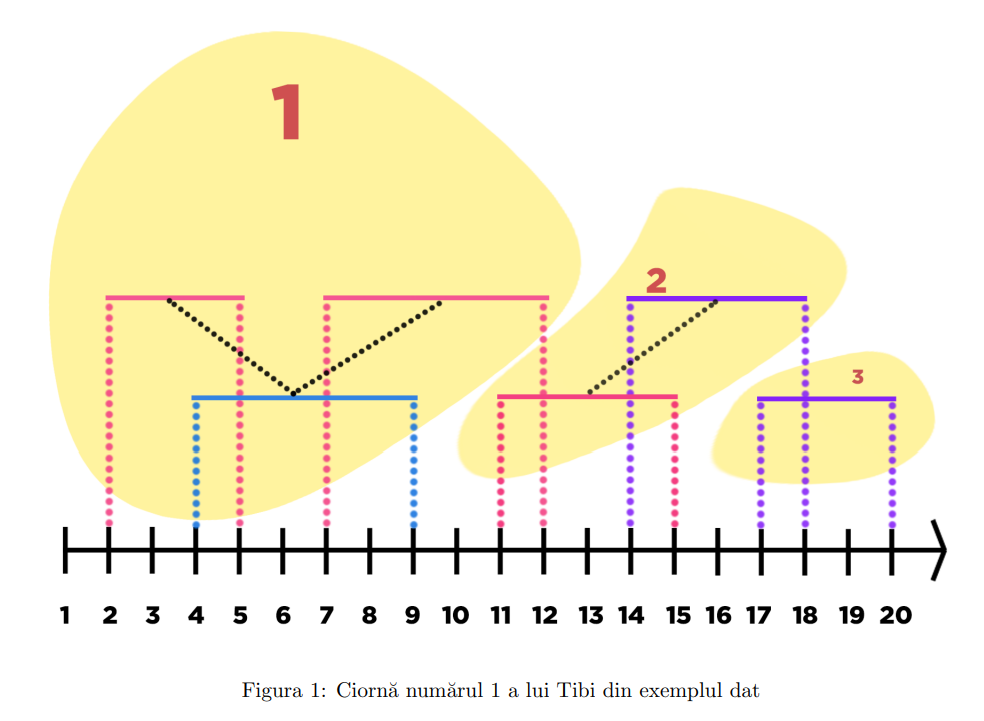
Explicație

În acest caz se formează următoarele conexiuni:

• Segmentul $1$, $[2, 5]$, este conectat direct cu segmentul $2$, $[4, 9]$ deoarece sunt de tipuri diferite și se intersectează pe intervalul $[4, 5]$ (au măcar un punct comun).
• Segmentul $2$, $[4, 9]$, este conectat direct cu segmentul $3$, $[7, 12]$ deoarece sunt de tipuri diferite și se intersectează pe intervalul $[7, 9]$ (au măcar un punct comun).
• Segmentul $3$ și segmentul $4$ au o intersecție nevidă, însă sunt de același tip deci nu sunt conectate direct.
• Restul segmentelor nu au intersecție comună cu segmentele $1$, $2$ și $3$, astfel segmentele $1$, $2$ și $3$ fac parte din același grup.
• Segmentul $4$, $[11, 15]$, este conectat direct cu segmentul $5$, $[14, 18]$ deoarece sunt de tipuri diferite și se intersectează pe intervalul $[14, 15]$ (au măcar un punct comun).
• Segmentul $4$ și segmentul $5$ au o intersecție nevidă, însă sunt de același tip deci nu sunt conectate direct.
• Restul segmentelor rămase nu au intersecție comună cu segmentele $4$ și $5$, astfel segmentele $4$ și $5$ fac parte din același grup.
• Segmentul $6$ nu este conectat cu niciun alt segment deci formează singur o grupă.

Astfel, se formează un total de $3$ grupuri.