Classical Hard Packing Problem

Task

$nume$ just got a job working at the airport. His job is to pack the luggage into the airplane. The luggage compartment of the airplane is a rectangle with height $n$ and width $4$. The luggages are $1 \times 4$ rectangles.

The packing procedure is as follows:

$nume$ sits at the top of the luggage compartment and throws luggages into it one by one.

For each luggage he can choose one of $5$ ways to orient the luggage.

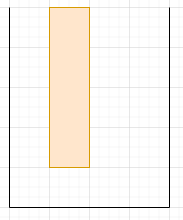
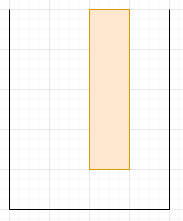
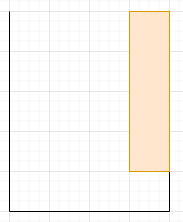
After being oriented, the luggage will fall towards the bottom of the luggage compartment until it hits either the bottom or another luggage. Note that once thrown, a luggage will always keep it's orientation.

$nume$ continues to throw luggages until there isn't any way to fit anymore luggages no matter how he orients them.

We define a possible configuration as any configuration of luggages that can be reached following this procedure.

$nume$ wants to know what is the sum of the number of luggages used over all the posible configurations.

Formally, let $cnt(x)$ be the number of luggages used in cofiguration $x$.
We want to know $\sum_{x \in possibleConfigurations} cnt(x)$.

Because this number can be very large, we want this number modulo $10^9 + 7$.

Input data

The first line will one number $n$, the height of the luggage compartment.

Output data

Print only one number, the requested sum modulo $10^9 + 7$.

Constraints and clarifications

$1 \leq n \leq 5000$

Example 1

stdin

2

stdout

2

Explanation

There is only one possible configuration. And this configuration uses 2 luggages.

Example 2

stdin

50

stdout

191158905