Se consideră matricea $A$ cu $n$ linii și $n$ coloane. O formație este compusă dintr-o subsecvență a unei linii $l$ și o subsecvență a unei coloane $c$ a matricei. Formația este determinată de către $3$ aspecte:

• doi indici $i_1$ și $i_2$, $1 \leq i_1 \leq i_2 \leq n$, ce reprezintă indicele de start, respectiv de final, al subsecvenței aflate pe coloana $c$.
• doi indici $j_1$ și $j_2$, $1 \leq j_1 \leq j_2 \leq n$, ce reprezintă indicele de start, respectiv de final, al subsecvenței aflate pe linia $l$.
• linia $l$ și coloana $c$ se intersectează într-un element $A[l][c]$, $i_1 \leq l \leq i_2, j_1 \leq c \leq j_2$ denumit nucleu, care obligatoriu are valoarea minimă a tuturor elementelor aflate în formație.

Puterea unei formații se calculează ca fiind produsul dintre valoarea nucleului și suma elementelor aflate în formație.

Cerință

1. Să se determine numărul total de formații din matrice $MOD \ 10^{9} + 7$.
2. Să se determine suma tuturor puterilor formațiilor din matrice $MOD \ 10^{9} + 7$.

Date de intrare

Fișierul de intrare formatie.in va conține pe prima linie un număr natural $C$, cu valorile $1$ sau $2$, reprezentând numărul cerinței.
Pe a doua linie, se va afla un număr natural $n$, reprezentând numărul de linii și de coloane.
Următoarele $n$ linii conțin fiecare câte $n$ numere, reprezentând elementele matricei.

Date de ieșire

Fișierul de ieșire formatie.out va conține pe prima linie un singur număr întreg $s$, reprezentând rezultatul cerut.

Observații

• O formație poate să fie formată dintr-un singur element.
• În cazul în care $i_1 = i_2$ sau $j_1 = j_2$, fiecare apariție a unui nucleu va determina o formație nouă.
• NU există formație în care intersecția dintre linie și coloană să fie vidă.

Restricții și precizări

• $1 \leq n \leq 500$
• $1 \leq A[i][j] \leq 1 \ 000$, $\forall i, j, 1 \leq i \leq n, 1 \leq j \leq n$

Punctare

Exemplul 1

formatie.in

1
3
9 8 4
3 3 4
1 9 5

formatie.out

50

Exemplul 2

formatie.in

2
3
9 8 4
3 3 4
1 9 5

formatie.out

2231

Explicații

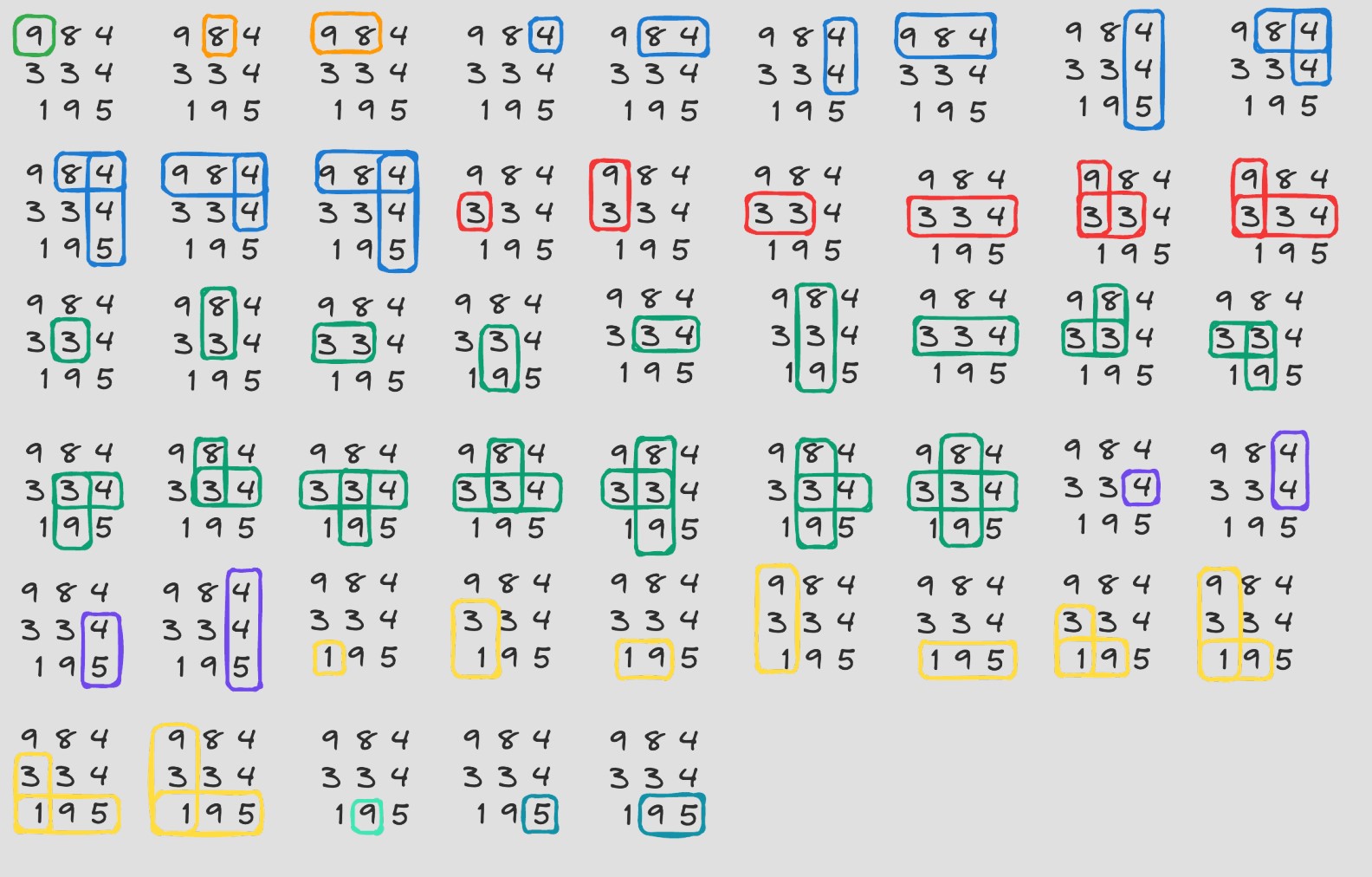
În desenul de mai sus, sunt evidențiate toate formațiile care se pot forma. În total, sunt $50$ de formații.
Pentru exemplul al doilea:
Puterea primei formații este $9 \cdot 9 = 81$.
Puterea celei de-a doua formații este $8 \cdot 8 = 64$.
Puterea celei de-a treia formații este $8 \cdot (8 + 9) = 8 \cdot 17 = 136$.
Puterea celei de-a patra formații este $4 \cdot 4 = 16$.
.
.
.
Puterea celei de-a $35$-a formații este $3 \cdot (3 + 3 + 4 + 9 + 8) = 81$.
. . .
Puterea celei de-a $50$-a formații este $5 \cdot (9 + 5) = 70$.
În total, suma tuturor puterilor este egală cu $2231$.

Formație	Explicație
	Formația este delimitată în conturul de culoare verde, și are $l = 2$, $c = 2$, $i_1 = 1$, $i_2 = 3$, $j_1 = 1$, $j_2 = 3$. Nucleul se află pe poziția $l = 2$, $c = 2$, și are valoarea $A[l][c] = 3$, fiind cea mai mică dintre toate elementele formației. Puterea acestei formații este $3 \cdot (8 + 3 + 9 + 3 + 4) = 3 \cdot 27 = 81$
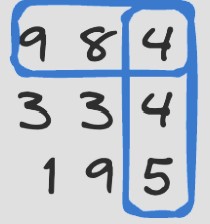	Formația este delimitată în conturul de culoare albastră, și are $l = 1$, $c = 3$, $i_1 = 1$, $i_2 = 3$, $j_1 = 1$, $j_2 = 3$. Nucleul se află pe poziția $l = 1$, $c = 3$, și are valoarea $A[l][c] = 4$, fiind cea mai mică dintre toate elementele formației. Puterea acestei formații este $4 \cdot (9 + 8 + 4 + 4 + 5) = 4 \cdot 30 = 120$
	Formația este delimitată în conturul de culoare galbenă, și are $l = 3$, $c = 1$, $i_1 = 1$, $i_2 = 3$, $j_1 = 1$, $j_2 = 2$. Nucleul se află pe poziția $l = 3$, $c = 1$, și are valoarea $A[l][c] = 1$, fiind cea mai mică dintre toate elementele formației. Puterea acestei formații este $1 \cdot (9 + 3 + 1 + 9) = 1 \cdot 22 = 22$
	Formația este delimitată în conturul de culoare albastră, și are $l = 1$, $c = 3$, $i_1 = 1$, $i_2 = 2$, $j_1 = 3$, $j_2 = 3$. Nucleul se află pe poziția $l = 1$, $c = 3$, și are valoarea $A[l][c] = 4$, fiind cea mai mică dintre toate elementele formației. Puterea acestei formații este $4 \cdot (4 + 4) = 4 \cdot 16 = 64$
	Formația este delimitată în conturul de culoare mov, și are $l = 2$, $c = 3$, $i_1 = 1$, $i_2 = 2$, $j_1 = 3$, $j_2 = 3$. Nucleul se află pe poziția $l = 2$, $c = 3$, și are valoarea $A[l][c] = 4$, fiind cea mai mică dintre toate elementele formației. Puterea acestei formații este $4 \cdot (4 + 4) = 4 \cdot 16 = 64$. Formația are în componența ei exact aceleași elemente ca și formația exemplificată anterior, dar are nucleul aflat pe o poziție diferită!