Floricel vrea să facă cât mai mulți bani. Ca să aibă suficienţi bani să-şi poată cumpăra un apartament, are de rezolvat o problemă care se poate modela astfel: El are intervale inițiale, date prin capetele lor. Floricel mai trebuie să creeze intervale noi, denumite intervale de acoperire.
Un interval inițial se consideră acoperit dacă există cel puțin un interval de acoperire cu intersecția dintre intervalul de acoperire și cel inițial de lungime cel puțin jumătate din lungimea intervalului inițial. De exemplu, intervalul este acoperit de mulțimea de intervale , dar nu este acoperit de mulțimea de intervale .
Cerință
Prietenul său, Ted, îi spune că are nevoie de mai multe provocări în viață să fie mai fericit, și îi pune întrebări de forma: “Dacă ai voie să creezi cel mult intervale de acoperire, care ar fi lungimea minimă a celui mai lung interval de acoperire astfel încât toate intervalele inițiale să fie acoperite? Și dacă poți, care este soluția minimă lexicografic? O soluție este minimă lexicografic dacă este minimă întâi după numărul intervalelor de acoperire, iar după aceea comparând intervalele după capetele de stânga și de dreapta, ordonând intervalele după capetele din stânga.”
Date de intrare
Prima linie a fișierului de intrare acoperire.in conține numărul . Următoarele linii conțin câte două numere naturale și , unde numerele de pe linia reprezintă capetele stânga și dreapta ale celui de-al -lea interval. Urmează o linie cu numărul , iar pe următoarele linii se află câte un număr , care reprezintă câte o întrebare a lui Ted, unde vrem să aflăm lungimea minimă a celui mai lung interval de acoperire, dacă putem crea cel mult intervale de acoperire.
Date de ieșire
Fișierul de ieșire acoperire.out trebuie să conțină răspunsuri în ordine. Pentru o întrebare cu dat, pe prima linie trebuie afișată lungimea celui mai lung interval de acoperire în condițiile cerute, pe următoarea linie trebuie să fie numărul de intervale de acoperire folosite (cel mult ), iar pe următoarele linii capetele stânga și dreapta ale intervalelor, ordonate după capătul stânga.
Dacă o valoare este număr întreg, trebuie afișată ca număr întreg, altfel trebuie afișată ca număr real cu fix o zecimală.
Restricții și precizări
- ;
- ;
- ;
- și suma tuturor este cel mult ;
- Se acordă puncte pentru un test doar dacă toate lungimile minime ale celui mai lung interval de acoperire sunt aflate corect. Dacă o soluție nu este corectă sau minimă lexicografic se va acorda totuși din punctajul unei întrebări. Toate întrebările unui test au aceeași valoare ca punctaj.
- Dacă vreți să afișați doar lungimea, puteți afișa ca numărul intervalelor din soluție.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 10 | |
| 2 | 10 | și intervalele inițiale sunt disjuncte. |
| 3 | 20 | |
| 4 | 20 | Intervalele inițiale sunt disjuncte, oricare două. |
| 5 | 40 | Fără restricții suplimentare. |
Exemplu
acoperire.in
5
0 2
1 4
1 2
3 5
3 6
3
1
2
3
acoperire.out
3.5
1
1 4.5
1.5
2
1 2.5
4 5.5
1.5
2
1 2.5
3 4.5
Explicație
Fișierul de intrare conține intervale inițiale, ilustrate cu roșu mai jos.
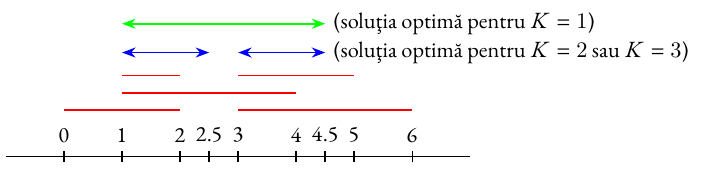
Pentru avem un singur interval de acoperire, de lungime , adică , și soluţia este minimă lexicografic.
Pentru , răspunsul din exemplul de mai sus reprezintă o soluție cu cel mai lung interval de acoperire de lungime . Soluția primește doar din punctajul celei de-a doua întrebări, pentru că nu este minimă lexicografic: înlocuirea intervalului cu reprezintă o soluție mai mică lexicografic.
Pentru soluția este minimă lexicografic, deoarece sunt necesare doar două intervale de acoperire.
Soluția obține din punctajul testului.
Epilog
“În final, Floricel și-a dat seama că lucrurile materiale sunt necesare dar nu suficiente pentru împlinire în viață. Acum că nu se mai ia după ce vede la alții, nu mai urmărește fake lifestyle, cringe și propagandă pe social media, iar scopurile spre care tinde sunt alese de el însuşi, pentru împlinirea sa și a celor din jur. Acum e cu adevărat fericit.”