Birocratie

Boris este un afacerist de succes, având contracte care aduc pe de o parte venituri (dobânzi, comisioane etc.) dar și obligații la taxe (impozite, rate etc.).

Boris s-a hotărât să viziteze o clădire de birouri. Clădirea are un singur nivel în care birourile sunt lipite unele de altele formând un caroiaj pătratic de dimensiune $N \times N$. Planul birourilor se poate reprezenta ca o matrice pătratică, unde birourile sunt elemente din matrice cu liniile și coloanele numerotate de la $1$ la $N$. Mai exact, la linia $i$, coloana $j$ se găsește biroul $(i, j)$.

Boris va intra în clădire prin biroul $(1, 1)$ și va trece printr-o serie de birouri. Traseul se va termina în biroul $(N, N)$. La trecerea dintr-un birou în altul se permite:

• pe același rând doar de la stânga la dreapta: $(i, j) \rightarrow (i, j + 1)$;
• pe aceeași coloană doar de sus în jos: $(i, j) \rightarrow (i + 1, j)$;
• în sens diagonal în următoarele două direcții:
  • $(i, j) \rightarrow (i + 1, j − 1)$, dar și
  • $(i, j) \rightarrow (i − 1, j + 1)$.

Totuși, Boris nu se va mai întoarce niciodată într-un birou din care a ieșit.

De câte ori Boris vizitează un birou $(i, j)$ el încheie un contract în valoare de $B(i, j)$ lei. Dacă $B(i, j) \gt 0$, atunci el primește $B(i, j)$ lei, iar dacă $B(i, j) < 0$, el plătește $−B(i, j)$ lei. Scopul lui Boris este acela de a ieși din clădire cu un câștig total maxim. Câștigul se definește ca fiind totalul de bani primiți minus totalul de bani plătiți pe traseu.

Atenție! Câștigul poate să fie și negativ dacă Boris plătește mai mult decât primește.

Cerință

Cunoscând planul birourilor și valorile $B(i, j)$ pentru $1 \leq i, j \leq N$ care îl așteaptă pe Boris în fiecare birou, ajutați-l să calculeze câștigul maxim pe care îl poate avea la ieșirea din clădire.

Date de intrare

Fișierul de intrare birocratie.in conține pe prima linie numărul $N$, iar pe următoarele $N$ linii câte $N$ numere întregi separate prin spații, reprezentând valorile $B(i, j)$ pentru $1 \leq i, j \leq N$.

Date de ieșire

Fișierul de ieșire birocratie.out va conține o singură linie pe care se află un singur număr întreg reprezentând câștigul maxim posibil.

Restricții și precizări

• $5 \leq N \leq 1 \ 000$;
• $-1 \ 000 \leq B(i, j) \leq 1 \ 000$ pentru $1 \leq i, j \leq N$.

Mai sus prin chenarul lui $B$ ne referim la elementele care se află pe prima/ultima linie și prima/ultima coloană.

Exemplu

birocratie.in

5
1 2 5 8 2
1 3 -10 2 1
0 9 1 -7 3
-2 3 4 -1 2
3 -4 2 3 1

birocratie.out

42

Explicație

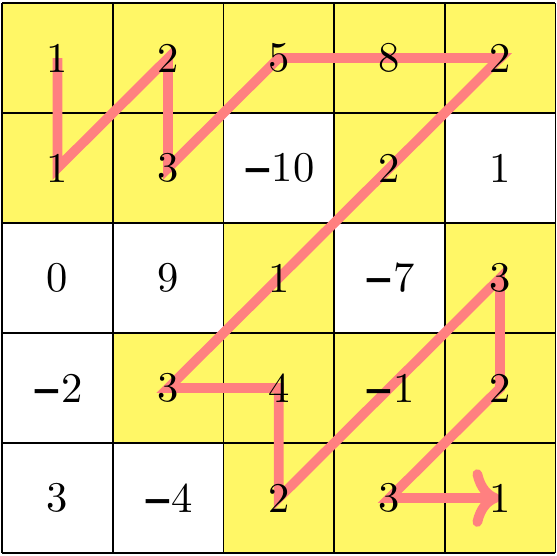
Câștigul maxim este 42, obținut adunând elementele evidențiate în traseul ilustrat mai jos.