Se cunosc înălțimile a vârfuri, plasate de la stânga la dreapta, în cadrul unui lanț muntos. Dacă plasăm o santinelă pe un vârf de o anumită înălțime, aceasta veghează vârful respectiv și maximum vârfuri la stânga și maximum vârfuri la dreapta acestuia, dar cu condiția ca înălțimile acestor vârfuri vegheate să fie mai mici sau egale cu înălțimea vârfului pe care se află santinela. Dacă există un vârf cu o înălțime strict mai mare la distanță mai mică sau egală cu , atunci santinela veghează doar până la acel vârf (exclusiv acel vârf).
Cerință
Date fiind , și înălțimile celor vârfuri, să se determine:
- Numărul maxim de vârfuri consecutive, începând de la primul vârf al lanțului muntos (inclusiv acest vârf), ce pot fi vegheate cu o singură santinelă.
- Numărul minim de santinele necesare ca toate vârfurile să fie vegheate.
Date de intrare
Fișierul de intrare santinele.in conține pe prima linie numărul cerinței, sau . Pe a doua linie, fișierul conține numerele și , cu semnificația din enunț. Pe a treia linie, fișierul conține numere, , reprezentând înălțimile celor vârfuri, în ordinea dispunerii lor de la stânga la dreapta, în cadrul lanțului muntos. Numerele aflate pe aceeași linie a fișierului de intrare sunt separate prin câte un spațiu.
Date de ieșire
Fișierul de ieșire santinele.out conține un singur număr. Dacă cerința este , conține numărul maxim de vârfuri determinate la această cerință. Dacă cerința este , conține numărul minim de santinele determinate la această cerință.
Restricții și precizări
- ;
- ;
- .
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 14 | |
| 2 | 14 | , par, . |
| 3 | 16 | și |
| 4 | 13 | și există , pentru care |
| 5 | 14 | , |
| 6 | 29 | , fără restricții suplimentare. |
Exemplul 1
santinele.in
1
8 2
6 10 5 7 8 5 4 4
santinele.out
4
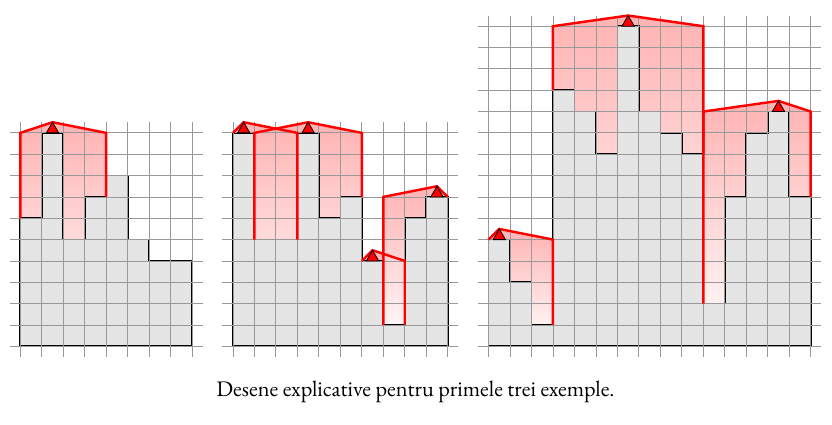
Explicație
Cerința este și . Santinela veghează vârful pe care este plasată, maximum două vârfuri la stânga și maximum două vârfuri la dreapta. Cu o singură santinelă putem acoperi maximum patru vârfuri, începând cu primul vârf, plasând santinela pe al doilea vârf.
Exemplul 2
santinele.in
2
10 2
10 5 5 10 6 7 4 1 6 7
santinele.out
4
Explicație
Cerința este și . Sunt necesare minimum santinele, pe care le putem amplasa pe vârfurile: primul, al -lea, al -lea, al -lea.
Exemplul 3
santinele.in
2
15 3
5 3 1 12 11 9 15 11 10 9 2 7 10 11 7
santinele.out
3
Explicație
Cerința este și . Sunt necesare minimum santinele. Le putem amplasa pe vârfurile: primul, al -lea, al -lea.
Exemplul 4
santinele.in
2
20 5
7 12 23 21 20 24 28 21 4 16 27 1 6 8 20 3 3 5 11 5
santinele.out
3
Explicație
Cerința este și . Sunt necesare minimum santinele. Le putem amplasa pe vârfurile: al -lea, al -lea, al -lea.