Pentru a atrage turiștii, primăria unui oraș a hotărât că va construi un parc acvatic imens cu n piscine. Parcul va avea o zonă acoperită și va fi înconjurat de un spațiu deschis pentru activități în aer liber.
Zona închisă va fi acoperită de o singură clădire de forma unui poligon, iar piscinele vor fi proiectate în vârfurile poligonului și vor putea comunica între ele prin m căi de acces care nu se vor intersecta. Căile de acces între două piscine pot fi de tipul 1: canal umplut cu apă în interiorul clădirii, sau de tipul 2: o alee în afara clădirii.
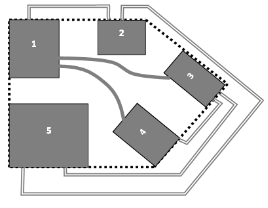
În exemplul alăturat prin linie punctată se delimitează partea acoperită a parcului. Avem 5 piscine, există 6 căi de acces: (1,2), (2,5), (1,4), (1,3), (3,4), (3,5), dintre care 2 sunt canale (tipul 1): (1,3) și (1,4), respectiv 4 sunt alei (tipul 2): (1,2), (2,5), (3,4) și (3,5).
Un alt proiect ce păstrează aceleași căi de acces, dar diferă prin tipul acestora, este să construim 4 canale: (1,2), (3,4), (3,5), (2,5) respectiv 2 alei: (1,3), (1,4).
În total putem construi 8 proiecte distincte cu aceste căi de acces. Două proiecte se consideră distincte dacă există cel puțin o cale de acces ce are tipuri diferite pe cele două proiecte.
Cerinţe
Cunoscând căile de acces între piscine, să se determine una dintre cerințele următoare:
- o modalitate de construire a căilor de acces, precizând tipul fiecăreia;
- numărul proiectelor distincte.
Date de intrare
Fișierul de intrare aquapark.in conține pe prima linie trei numerele separate prin câte un spațiu c n m reprezentând în această ordine tipul cerinței, numărul piscinelor respectiv numărul căilor de acces. Următoarele m linii conțin câte două numere x și y, reprezentând o cale de acces între piscina x și piscina y.
Date de ieşire
Fișierul de ieșire aquapark.out va conține în funcție de valoarea lui c următoarele informații:
- dacă
c=1: pe m linii se vor tipări câte trei numere separate prin câte un spațiux y t, semnificând că între piscinaxși piscinayexistă o cale de acces de tipult(1-canal,2-alee). Fiecare muchie citită din fișierul de intrare va trebui să apară exact o dată în fișierul de ieșire, indiferent de ordinea citirii. - dacă
c=2: se va tipări un singur număr ce va semnifica numărul proiectelor distincte modulo666013.
Restricţii și precizări
1 ≤ n ≤ 70 0001 ≤ m ≤ 100 000- Între două piscine există cel mult o cale de acces
- Nu există o cale de acces de la o piscină la ea însăşi
- Se asigură că pentru datele de test există cel puțin o soluție,
- Dacă există mai multe soluții se poate afișa oricare dintre acestea.
- Pentru teste în valoare de
16puncten, m ≤ 15 - Pentru alte teste în valoare de
49de puncten ≤ 1000, m ≤ 1500 - Punctajul maxim al problemei este de
100de puncte dintre care10puncte din oficiu.
Exemplu
aquapark.in
1 5 6
1 2
2 5
1 4
3 1
4 3
5 3
aquapark.out
1 2 1
1 3 1
1 4 1
2 5 2
3 4 1
3 5 2
aquapark.in
2 5 6
1 2
2 5
1 4
3 1
4 3
5 3
aquapark.out
8
Explicații
Pentru primul test:
c=1, se cere o modalitate de construcție a căilor de acces:
Avem cale de acces de tip 1 (canale) între piscinele (1,2), (1,3), (1,4) și (3,4). Avem cale de acces de tip 2 (alee) între piscinele (2,5) și (3,5)..
Vezi desenul de mai sus.
Pentru al doilea test:
Avem 8 modalități distincte de a construi căile parcului acvatic:
| Soluție | căi de tipul 1 | căi de tipul 2 |
|---|---|---|
| 1 | (1,2) (1,3) (1,4) (3,4) | (2,5) (3,5) |
| 2 | (1,3) (1,4) (3,4) | (1,2) (2,5) (3,5) |
| 3 | (1,2) (1,3) (1,4) | (2,5) (3,5) (3,4) |
| 4 | (1,3) (1,4) | (1,2) (2,5) (3,5) (3,4) |
| 5 | (2,5) (3,5) | (1,2) (1,3) (1,4) (3,4) |
| 6 | (1,2) (2,5) (3,5) | (1,3) (1,4) (3,4) |
| 7 | (2,5) (3,5) (3,4) | (1,2) (1,3) (1,4) |
| 8 | (1,2) (2,5) (3,5) (3,4) | (1,3) (1,4) |