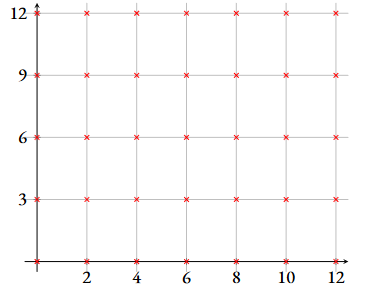
For every two positive integers we define to be those points for which divides and divides , and where are non-negative integers. In other words, the points of can be thought of as those points reachable from by moving a multiple of steps to the right, and a multiple of steps up. For example, looks like this.
Task
Given and a list of points with integer coordinates in the plane, answer the following question: For how many positive integers does contain at least of the points?
Input data
The first line of the input contains and . The next lines contain the points .
Output data
The first line of the output should contain the answer to the question.
Restrictions
| # | Points | Restrictions |
|---|---|---|
| 1 | 16 | All the values from input are at most |
| 2 | 11 | All the values from input are at most |
| 3 | 15 | for all the points |
| 4 | 21 | The sequence contains pairwise distinct elements. |
| 5 | 37 | No further restrictions. |
Example 1
stdin
3 2
1 3
3 6
4 2
stdout
1
Explanation
In the first example, only contains at least points.
Example 2
stdin
5 2
2 2
5 10
6 4
15 5
1 7
stdout
3
Explanation
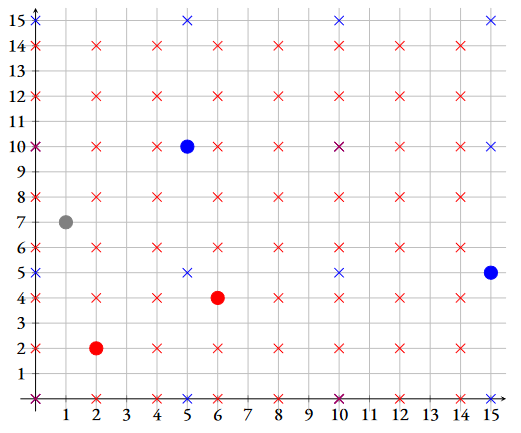
Here, contains all the points, has the first and the third point and has the second and the fourth point. Below is a grid showing all the lattices. is the underlying grid, is marked by , and is marked by . The points in all three lattices are marked by . The points in the input are marked by filled-in circles , with the colour showing which grid they belong to: if a point is only in it is , if it is in and it is , and if it is in and it is .