Scriitorul, Alan Wake, s-a pierdut în propriul palat al minții. Acesta este ca un labirint care are un loc de ieșire. Sunt zone din labirint care sunt blocate. Din fericire, are la el o lampă cu care se poate teleporta în dimensiunea întunecată, care este la rândul ei un labirint. Alan poate să sară dintr-o dimensiune în alta, păstrându-și poziția, dar lampa este pe terminate, și are un număr limitat de utilizări.

Cele două labirinte sunt reprezentate de matrice de $0$ și $1$. Wake se poate mișca cu o poziție în labirint, în 4 direcții: nord, sud, est, vest. Nu se poate mișca pe diagonală. De asemenea, poate sări între cele două dimensiuni, păstrându-și poziția. Schimbarea se poate face doar dacă în ambele dimensiuni, pătratul unde se face teleportarea este liber. În codificarea labirintului, $0$ înseamnă liber iar $1$ este zid.

Cerință

Alan Wake dorește să găsească cel mai scurt drum în labirint și să afle adevărul.

El a încercat să scrie un program C++ care să îi îndeplinească această dorință, dar conține câteva bug-uri și nu le poate identifica. Corectați-i programul lui Alan Wake. Îl puteți găsi aici sau în secțiunea „Atașamente” din lateral.

Indicație

Pentru problema labirintului, de regulă, se folosește algoritmul lui Lee (Breath First Search/Căutare în lățime), care folosește o coadă ca structură de date. Cu toate acestea, în problema noastră avem două labirinturi (al luminii și al întunericului), iar teleportarea este limitată.

Soluția este să reprezentăm spațiul ca o matrice 3D, unde primul strat este labirintul luminii, al doilea este labirintul întunercului, al treilea este din nou labirintul luminii, acestea alternând. Adâncimea matricei 3D este numărul de schimbări maxime plus $1$. Valoarea adâncimii reprezintă numărul de teleportări folosite. Pe langă cele 4 mișcări pe un strat, adăugăm o nouă mișcare, anume, trecerea cu un strat mai jos, pe aceeași poziție, reprezentând teleportarea. Personajul poate coborî, dar nu poate urca.

Astfel, simulăm tranziția între dimensiuni cu trecerea prin straturi. Dacă Wake se află în primul strat, înseamnă că a folosit $0$ teleportări. Dacă este pe ultimul, înseamnă că le-a folosit pe toate, și nu se mai poate mișca în adâncime.

Spre exemplu, următoarele mișcări între două labirinturi:

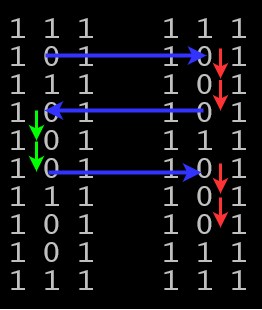
În spațiul 3D, aceleași mișcări arată astfel:

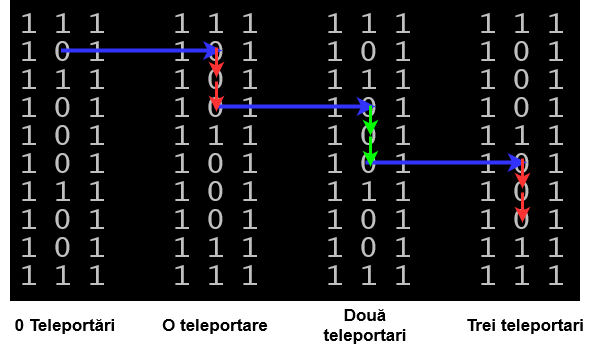
Date de intrare

Pe prima linie se citește $switch\_max$ — numărul maxim de teleportări pe care le poate face Wake.

Pe a doua linie se citesc $n$ și $m$ — numărul de linii respectiv coloane ale labirintului.

Se lasă o linie goală, după care se citește labirintul luminii — $n$ linii a câte $m$ numere fiecare.

Se lasă încă o linie goală, după care se citește labirintul întunericului — $n$ linii a câte $m$ numere fiecare.

Se lasă o linie goală. Pe următoarea linie se citesc $start_x$ și $start_y$ — linia respectiv coloana unde se află Wake în labirintul luminii, indexate de la $0$. Pe următoarea linie se citesc $target_x$ și $target_y$ — linia respectiv coloana unde trebuie să ajungă Wake în labirintul luminii, indexate de la $0$.

Date de ieșire

Se va afișa pe ecran lungimea drumului cel mai scurt, incluzând și teleportările.

Daca nu se poate ajunge la final sau nu sunt destule teleportări, se afișează -1.

Restricții și precizări

• $3 \leq n, m \leq 50$
• $0 \leq switch\_max \leq 15$
• Se garantează că matricele sunt bordate la margini cu $1$.
• Pozițiile de start și de final sunt zone libere în labirintul luminii.

Exemplul 1

stdin

4
10 3

1 1 1
1 0 1
1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 0 1
1 0 1
1 1 1

1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 1 1

1 1
8 1

stdout

11

Explicație

Alan face $7$ mișcări în jos pentru a ajunge la final. Iar, pentru a trece de ziduri, face $4$ teleportări:

• din lumină în întuneric, coordonatele $(1, 1)$;
• din întuneric în lumină, coordonatele $(3, 1)$;
• din lumină în întuneric, coordonatele $(5, 1)$;
• din întuneric în lumină, coordonatele $(7, 1)$.

În total (incluzând teleportările) sunt $7 + 4 = 11$ mișcări.

Exemplul 2

stdin

3
10 3

1 1 1
1 0 1
1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 0 1
1 0 1
1 1 1

1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 0 1
1 0 1
1 0 1
1 1 1
1 1 1

1 1
8 1

stdout

-1

Explicație

La fel ca la exemplul $1$, dar nu avem destule teleportări și nu există vreun mod de a ajunge de la start la finish.

Exemplul 3

stdin

4
15 9

1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 0 1
1 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 1 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 1
1 0 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1
1 0 0 0 0 0 0 0 1
1 0 1 1 1 1 1 1 1
1 0 1 0 0 0 0 0 1
1 1 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 1 1 0 0 0 0 0 1
1 0 1 0 0 0 0 0 1
1 1 1 1 1 1 1 1 1

1 1
13 1

stdout

28