Tanaka and Lulu are a bit nervous for the cook-off contest (after all, it is the most important contest in all of Info(1)cup Kingdom). So, in order to relax, they decided to play a game of hide-and-seek. Because they are as competitive as they are, they are playing this game on the largest surface available: the entire Info(1)cup Kingdom. The Info(1)cup Kingdom can be viewed as a network of n towns and m two-way roads. Two towns may be connected by at most one road, and no road connects a town to itself. It is possible to reach any town from any other town. Lulu and Tanaka will hide in towns.
Lulu and Tanaka have k friends which will try to stop them from finding each other. The kingdom has a special property: as long as Lulu and Tanaka hide in different towns, the k friends can each block a road, such that there is no way for Lulu to reach Tanaka. Friends are allowed to do nothing (to not block a road). For example, suppose that the kingdom has 5 towns, with roads between towns (1, 2),(1, 3),(1, 4),(2, 5),(3, 5),(4, 5). The kingdom is pictured below:
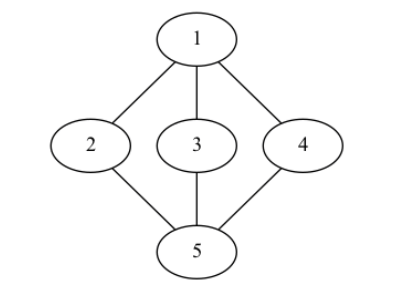
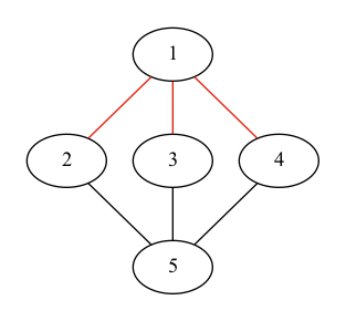
In this case it would be possible for them to have k = 3 friends. If Lulu or Tanaka hide in towns 2, 3 or 4, then their friends could block the 2 roads that are connected to these towns. For example, if one of them hides in 2, by blocking the roads marked with red below, their friends can make it so that Lulu cannot reach Tanaka:
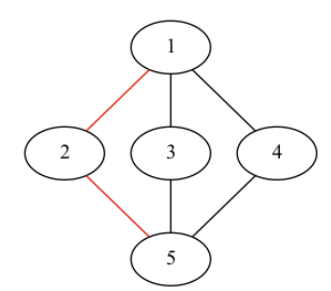
On the other hand, if Lulu hides in town 1, and Tanaka hides in town 5, then the friends could block roads (1, 2),(1, 3),(1, 4), as shown below:
Likewise, they could have k = 3, k = 4, or even k = 5 friends. On the other hand, they cannot have k = 2 friends: if Lulu hides in town 1 and Tanaka in town 5, then only 2 friends cannot block roads so as to stop Lulu from being able to reach Tanaka.
Each town has a different overall visibility (some towns are at a higher altitude, and thus can be seen from more places). Let be the visibilities of the towns.
Being very dedicated to hide-and-seek, Lulu has already observed a typical day in the Info(1)cup Kingdom, and knows that during the day the visibility of an intersection may change (due to the position of the sun, traffic, etc.). More precisely, Lulu wants to process q different events. Each event affects a certain town. If an event affects town i, then , the visibility of town i, becomes
.
For every event, he is interested in the value of after the operation.
Input
The first line of the input contains the integers n (the number of towns), m (the number of roads) and k (the number of friends Lulu and Tanaka have). The second line contains an array v, where v[i] is the initial visibility of town i, for 1 ≤ i ≤ n. The next m lines each contain a pair of integers u, v, denoting that there’s a two-way road between towns u and v. Line m + 3 contains an integer q (the number of events). The next line contains q numbers, each denoting an event.
Output
The line number i contains the value for the i-th query.
Restrictions
1 ≤ k ≤ 5
Subtask 1 (23 points)
1 ≤ n, q ≤ 2000
Subtask 2 (21 points)
Subtask 3 (25 points)
k = 1
Subtask 4 (31 points)
- No further restrictions.
Examples
stdin
5 6 3
1 2 3 4 5
1 2
1 3
1 4
2 5
3 5
4 5
3
1 5 3
stdout
10
14
27
Explanations
The network of towns is the one represented in the diagram below.
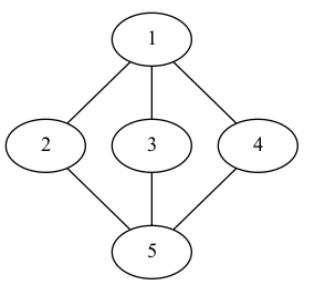
After the first query, the visibility of town 1 becomes 1 + 2 + 3 + 4 = 10. After the second query, the visibility of town 5 becomes 5 + 2 + 3 + 4 = 14. After the third query, the visibility of town 3 becomes 3 + 10 + 14 = 27.