soc

Un grup de $N$ oameni de afaceri s-au întâlnit cu ocazia unei conferinţe. Unii dintre ei sunt duşmani, alţii nu (de prietenie nu se prea pune problema când este vorba de afaceri). Fiecare dintre ei are un cont în bancă ce conţine o anumită sumă exprimată în euro. De fiecare dată când se întâlnesc, se gândesc cum să iniţieze o nouă afacere.
De data aceasta s-au decis să înfiinţeze o societate, la care acţionarii să fie o parte dintre ei, astfel încât oricare doi oameni de afaceri care sunt acţionari ai societăţii să nu fie duşmani, iar capitalul societăţii (egal cu totalul sumelor din conturile acţionarilor) să fie maxim. Pentru a determina acţionarii acestei societăţi, v-au angajat pe dumneavoastră şi, dacă le veţi da răspunsul în timp util, veţi fi recompensat cu o sumă frumoasă.
Înainte de a vă apuca de treabă, cei $N$ oameni de afaceri v-au pus la dispoziţie informaţii referitoare la conturile lor din bancă şi la relaţiile de duşmănie dintre ei. Analizând problema, aţi ajuns la concluzia că relaţiile de duşmănie pot fi reprezentate sub forma unui graf neorientat cu $N$ vârfuri (corespunzătoare celor $N$ oameni de afaceri); între două vârfuri diferite există o muchie, dacă cei doi oameni de afaceri corespunzători celor două vârfuri din graf sunt duşmani (duşmănia este reciprocă). Graful are o structură specială, mai exact el este un graf cordal. Un graf se numeşte graf cordal dacă îndeplineşte una dintre următoarele $2$ condiţii:

1. Este un graf cu un singur nod.
2. Se obţine inserând un nod nou $X$ într-un graf cordal $G$, astfel: se alege o submulţime de noduri din $G$, cu proprietatea că există muchie între oricare două noduri din submulţime (submulţimea poate conţine şi doar un singur nod), şi se introduce câte o muchie între nodul nou inserat $X$ şi fiecare nod din submulţime.
   

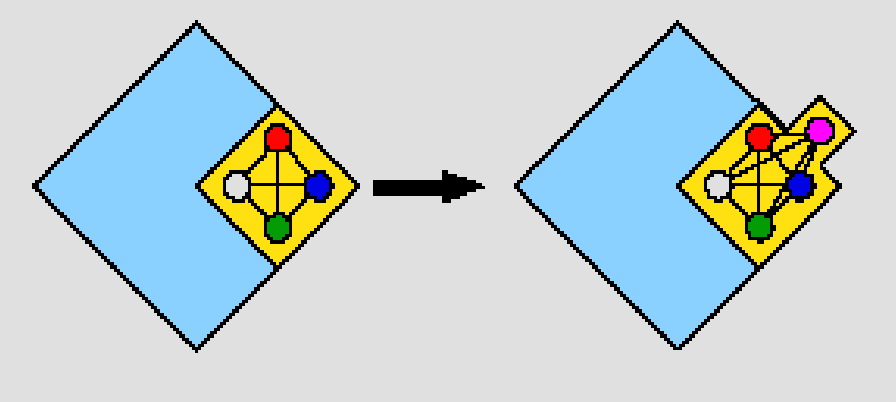
O definiţie echivalentă a grafurilor cordale este următoarea: un graf se numeşte graf cordal dacă este conex şi orice ciclu elementar (ce conţine fiecare nod al grafului cel mult o dată) având cel puţin $4$ noduri conţine cel puţin o « coardă » (o muchie între două noduri care fac parte din ciclu, dar nu sunt adiacente pe ciclu).
În continuare, iată câteva exemple de grafuri cordale şi grafuri care nu sunt cordale :

Date de intrare

Pe prima linie a fişierului de intrare soc.in se află numerele întregi: $N$ şi $M$, separate printr-un spaţiu. Pe următoarea linie se află numerele întregi $E_i,i=1,2,..,N$, separate prin câte un spaţiu, reprezentând sumele din conturile celor $N$ oameni de afaceri. Numărul EK reprezintă suma din contul afaceristului numerotat cu $K$. Pe următoarele $M$ linii se află câte două numere întregi $a$ şi $b$ din intervalul $[1,N]$, având semnificaţia că oamenii de afaceri numerotaţi cu $a$ şi, respectiv, $b$ sunt duşmani.

Date de ieşire

În fişierul soc.out veţi afişa, pe prima linie, capitalul maxim al societăţii. Pe următoarea linie veţi afişa numărul $A$, reprezentând numărul de acţionari ai societăţii. Pe cea de-a treia linie veţi afişa numerele oamenilor de afaceri care vor fi acţionari, separate prin câte un spaţiu. Dacă există mai multe posibilităţi de a alege acţionarii societăţii astfel încât capitalul acesteia să fie maxim, puteţi afişa oricare din ele. Numerele oamenilor de afaceri pot fi afişate în orice ordine (nu neapărat în ordine crescătoare).

Restricții și precizări

• $2 \leq N \leq 256$
• $1 \leq M \leq \frac{N \cdot (N-1)}{2}$
• $1 \leq E_i \leq 1 \ 000 \ 000$, pentru $i=1,2,..,N$
• Dacă determinaţi doar capitalul maxim al societăţii, dar nu şi acţionarii acesteia, veţi primi $60 \%$ din punctajul corespunzător testului respectiv.
• În cazul a $20 \%$ din fişierele de test, $M=N-1$
• În cazul a $60 \%$ din fişierele de test, fiecare componentă biconexă a grafului dat va conţine maxim $15$ noduri

Exemplu

soc.in

16 31
4 4 4 3 1 5 5 3 2 3 1 1 3 5 4 4
1 3
1 8
1 9
1 10
2 4
2 7
2 13
3 4
3 7
3 8
3 9
3 10
3 13
3 16
4 7
4 13
5 6
5 7
5 15
6 7
6 15
7 11
7 13
7 15
8 9
9 10
10 12
10 14
10 16
11 15
12 14

soc.out

23
6 
1 2 6 11 14 16