Să considerăm secvenţe de grafuri neorientate de tipurile următoare:
- Tipul
Secvenţa grafurilor de tip se construieşte în modul ce se poate deduce din exemplele următoare:

Observaţi că graful are vârfuri. - Tipul
Secvenţa grafurilor de tip se construieşte după modelul următor:
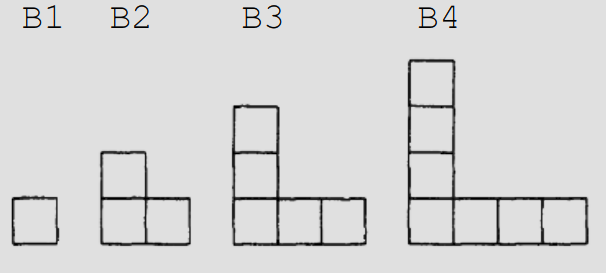
- Tipul
Secvenţa grafurilor de tip se construieşte după modelul următor:
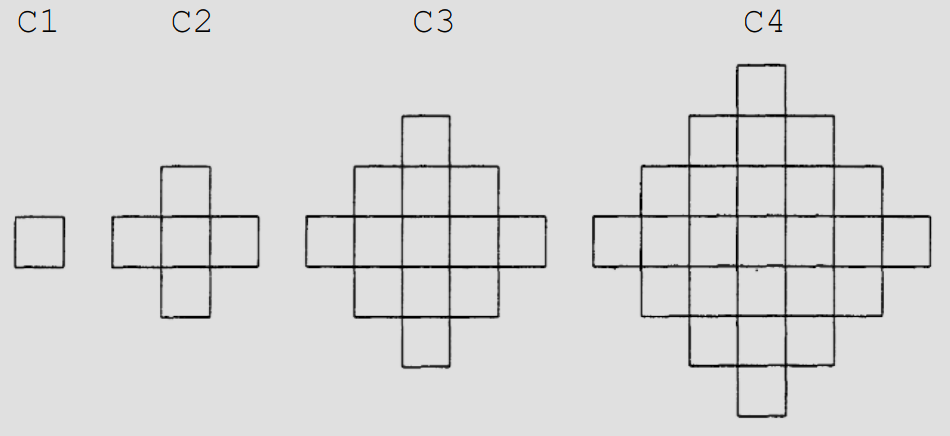
Se numeşte cuplaj perfect în graf o modalitate de a alege muchii ale grafului astfel încât oricare vârf din graf să fie incident cu exact o muchie aleasă. Două cuplaje sunt distincte dacă există o muchie care aparţine unui cuplaj, dar nu aparţine celuilalt.
Cerinţă
Dat fiind un graf de unul dintre tipurile din enunţ, să se determine numărul de cuplaje perfecte distincte ale grafului respectiv.
Date de intrare
Fişierul de intrare perfect.in conţine o singură linie pe care se află un caracter şi un număr natural nenul , separate printr-un spaţiu. Caracterul poate fi sau şi indică tipul grafului. Numărul natural indică numărul de ordine al grafului în secvenţa de grafuri de tipul specificat de caracter.
Date de ieşire
Fişierul de ieşire perfect.out va conţine o singură linie pe care va fi scris numărul de cuplaje perfecte ale grafului din fişierul de intrare.
Restricții și precizări
Exemplul 1
perfect.in
A 4
perfect.out
5
Explicație
Cele cuplaje perfecte ale grafului sunt:
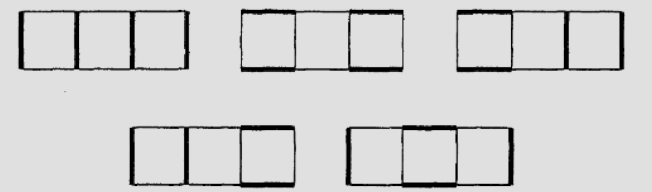
Exemplul 2
perfect.in
B 2
perfect.out
4
Explicație
Cele cuplaje perfecte ale grafului sunt:

Exemplul 3
perfect.in
C 2
perfect.out
8
Explicație
Cele cuplaje perfecte ale grafului sunt:
