import

Ca orice ţară civilizată, România importă diferite produse din alte ţări. În acest scop se efectuează $M$ transporturi, fiecare transport plecând dintr-un oraş din afara ţării şi având ca destinaţie finală un oraş din România. Orice transport este efectuat de un camion ce aparţine fie firmei Alfatrans, fie firmei Betatrans.

Putem presupune că oraşele sunt numerotate de la $1$ la $N$, oraşele $1..K$ fiind din Romania, iar oraşele $K+1..N$ din alte ţări. Între aceste oraşe există $N-1$ şosele bidirecţionale astfel încât între oricare $2$ oraşe există exact un drum (format din una sau mai multe şosele) şi orice drum de la un anumit oraş din România către un oraş din altă ţară trece prin oraşul $1$, în acest oraş aflându-se vama.

Pe parcursul drumului oricărui transport, la trecerea printr-un oraş şoferul camionului trebuie să plătească anumite taxe şi trebuie să comercializeze o parte din produsul transportat, astfel încât să obţină un profit fixat de primăria oraşului respectiv.

Guvernul României a stabilit pentru fiecare transport profitul total minim ce trebuie obţinut. Profitul total se obţine însumând profiturile obţinute în fiecare oraş prin care trece camionul pe drumul de la oraşul de plecare la oraşul destinaţie (inclusiv oraşul de plecare şi oraşul destinaţie).

Patronul Alfatrans are numeroase relaţii internaţionale şi poate manipula primăria fiecărui oraş. Astfel, el poate să stabilească pentru fiecare oraş $i$ profitul $P_i$ care trebuie să fie obţinut la trecerea unui camion prin oraşul respectiv.

Pentru a discredita firma Betatrans, patronul firmei Alfatrans doreşte să stabilească $P_i$ pentru fiecare oraş $i$ astfel încât orice transport executat de camioane Alfatrans să aducă un profit mai mare sau egal cu profitul minim stabilit pentru acel transport şi orice transport executat de camioane Betatrans să aducă un profit strict mai mic decât profitul stabilit.

Cerinţă

Pentru un număr considerabil de acţiuni la Alfatrans şi pentru a obţine $100$ de puncte, trebuie să-l ajutaţi pe patronul firmei Alfatrans să stabilească pentru fiecare oraş profitul impus de primărie astfel încât firma Betatrans să fie discreditată.

Date de intrare

Pe prima linie a fişierului de intrare import.in sunt scrise numerele naturale $N \ M \ K$ separate prin câte un spaţiu, având semnificaţia din enunţ. Următoarele $N-1$ linii conţin câte două numere naturale $a, b$ separate printr-un spaţiu, cu semnificaţia că există o şosea bidirecţională de la oraşul $a$ la orasul $b$. Următoarele $M$ linii descriu transporturile după cum urmează. Fiecare linie conţine $4$ numere $a \ b \ c \ d$separate prin câte un spaţiu cu semnificaţia "se face transport de la oraşul $a$ la oraşul $b$ executat de firma $x$, iar profitul minim ce trebuie asigurat pentru acest transport este $c$". Firma $x$ este Alfatrans dacă $d=0$ şi respectiv Betatrans dacă $d=1$. Se garantează că pentru orice transport $a$ este un oraş din afara ţării, iar $b$ este un oraş din România.

Date de ieşire

Fişierul import.out va conţine o singură linie pe care se vor scrie $n$ numere separate prin exact câte un spaţiu. Cel de al $i$-lea număr de pe linie reprezintă $P_i$, profitul stabilit de patronul Alfatrans pentru oraşul $i$. Dacă aceste valori vor face ca firma Betatrans să nu respecte cerinţele guvernului, iar firma Alfatrans să respecte în totalitate aceste cerinţe veţi obţine punctajul maxim pe test.

Restricții și precizări

• $2 < N < 222$
• $1 < K < N$
• $0 < M < K \times (N-K)$
• Profitul minim ce trebuie asigurat pentru fiecare transport este un număr întreg cuprins între $-10^{9}$ şi $10^{9}$
• Profiturile $P_i$ trebuie să fie numere întregi cuprinse între $-100 \ 000$ şi $100 \ 000$.
• Se garantează existenţa unei soluţii.

Exemplu

import.in

7 4 4
1 3
3 2
3 4
1 5
1 6
6 7
6 2 10 0
6 3 5 1
7 4 7 0
5 4 -2 1

import.out

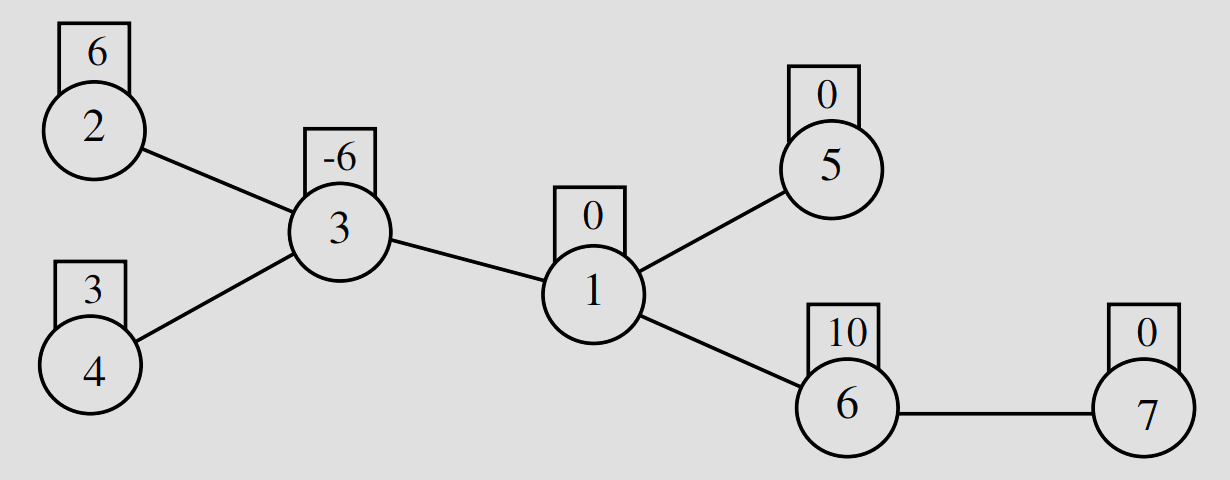
0 6 -6 3 0 10 0

Explicație

Primul transport trece prin oraşele $6 \ 1 \ 3$ şi $2$ obţinând un profit de $10+0-6+6=10$ deci respectă condiţiile din enunţ.
Al doilea trece prin $6 \ 1 \ 3$ obţine un profit de $10+0-6=4<5$ şi de asemenea respectă condiţiile din enunţ
Al treilea drum trece prin oraşele $7 \ 6 \ 1 \ 3 \ 4$, obţine un profit de $0+10+0-6+3=7$, iar ultimul drum trece prin $5 \ 1 \ 3 \ 4$ cu un profit de $0+0-6+3= -3 < -2$