Sumex

You are given a sequence $a_1, \ldots, a_n$ and $q$ independent queries. For each query, you are provided with two natural numbers $l$ and $r$. Consider the subsequence $a_l, a_{l+1}, \ldots, a_{r}$. Your task is to calculate the sum of the minimum excluded numbers of all subsequences of the form $a_{i}, a_{i+1}, \ldots, a_{j}$, for $l \leq i \leq j \leq r$.

The minimum excluded number of a subsequence is the smallest natural number that does not appear in the subsequence. For example, for the subsequence $0, 1, 4, 2$, it is $3$, but for the subsequence $1, 2, 3, 4$, it is $0$.

Input data

The first line of the input contains the numbers $n$ and $q$. The second line contains $n$ numbers $a_1, a_2, \dots, a_n$, which represent the initial sequence. Each of the following $q$ lines contains two numbers $l$ and $r$, which describe, respectively, each query.

Output data

The output should contain the answers to the $q$ queries in order, each on a new line.

Constraints

• $1 \leq n, q \leq 2 \cdot 10^5$
• $0 \leq a_i \leq n$
• $1 \leq l \leq r \leq n$

Subtask 1 (3 points)

• $1 \leq a_i \leq n$

Subtask 2 (10 points)

• $1 \leq q \leq 200$
• $r - l \leq 200$ for each query

Subtask 3 (12 points)

• $1 \leq n \leq 5 \ 000$

Subtask 4 (15 points)

• Each number from $0$ to $n - 1$ appears exactly once in $a_1, a_2, \dots, a_n$.

Subtask 5 (15 points)

• $0 \leq a_i \leq 100$
• There are no two queries $i$ and $j$ such that $l_i < l_j$ and $r_j < r_i$.

Subtask 6 (22 points)

• $l = 1$ for each query.

Subtask 7 (23 points)

• No additional constraints.

Example

stdin

6 3
0 1 2 0 1 3
1 2
3 5
1 6

stdout

3
7
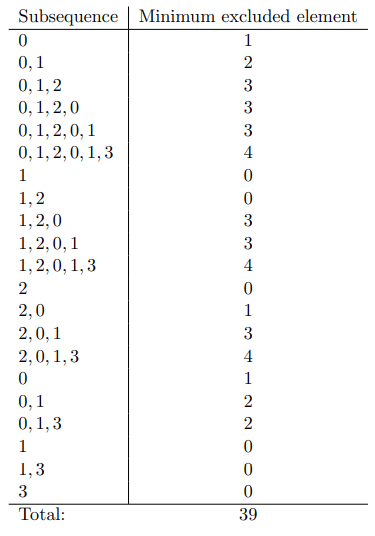
39

Explanations

Explanations for the first two queries:



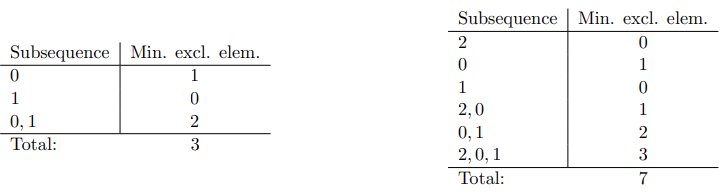
Explanation for the third query: