team

Sâmbăta o petrec cu prietenii la discoteca ”Why not“ din centrul oraşului. De acolo plecăm în zori $p$ persoane, în gaşcă, şi trebuie să ajungem fiecare acasă. Atât la discotecă, la punctele de destinaţie ale membrilor găştii, precum şi în alte puncte ale oraşului se află staţii de Team-Taxi pe care le putem folosi în drumul spre casă, plătind frăţeşte pe fiecare segment de drum o sumă fixă pe care o pretinde şoferul maşinii (în funcţie de lungimea drumului şi nu în funcţie de numărul de pasageri).

În orice staţie pot părăsi gaşca numai cei care au ajuns la destinaţie, în acest caz grupurile omogene formate urmând să se despartă (pentru că au dispărut oamenii de legătură) şi să ia în continuare taxiuri cu diferite destinaţii. Două grupuri omogene diferite pot merge în aceeaşi destinaţie, dar utilizând taxiuri diferite.

Numim grup omogen o formaţie de persoane cu numere de ordine consecutive. De exemplu, pentru $p=6$, de la discotecă porneşte gaşca în formaţia $1 \ 2 \ 3 \ 4 \ 5 \ 6$. Dacă la o staţie se opreşte persoana numărul $3$, atunci se formează două grupuri omogene, $1 \ 2$ şi $4 \ 5 \ 6$. Ei se despart luând două taxiuri diferite. Două grupe formate din $1 \ 4 \ 5$ şi $2 \ 6$ nu sunt omogene.

Atâta timp cât $k$ persoane merg cu un taxi pe un segment pe care orice şofer cere invariabil suma $c$, contribuţia fiecăruia pe acel segment este $c/k$. Dacă o persoană merge singură cu un taxi pe segmentul respectiv, ea va trebui să plătească singură întreaga sumă.

Cerinţă

Ştiind numărul de persoane, reţeaua de staţii de taxiuri, costurile de transport pe fiecare segment al reţelei şi punctele de destinaţie ale fiecărui membru al găştii, se cere să se determine costul minim pe care îl pot plăti în total membrii găştii astfel încât, utilizând taxiurile în maniera descrisă, fiecare să ajungă acasă.

Date de intrare

Din fişierul team.in se citesc:

• $p$ numărul de persoane din gaşcă ce pleacă de la discotecă, de pe linia $1$;
• $n$ numărul de staţii de taxi din oraş, de pe linia $2$; staţiile sunt numerotate de la $1$ la $n$;
• $m$ numărul de segmente ce leagă direct câte două staţii, de pe linia $3$;
• $m$ triplete de forma $i j c$ ($i$ şi $j$ sunt staţiile între care se consideră segmentul, iar $c$ costul de transport pe segmentul respectiv), de pe următoarele $m$ linii;
• $d_1 d_2 … d_p$ staţiile de destinaţie ale membrilor găştii (nu neapărat distincte), de pe ultima linie.

Date de ieşire

Fişierul team.out va conţine o singură linie cu un număr reprezentând costul minim determinat.

Restricții și precizări

• $1 \leq p \leq 50$
• $2 \leq n \leq 500$
• $1 \leq i, j \leq n$
• $0 \leq c \leq 1 \ 000$
• $1 \leq d_1, d_2, …, d_p \leq n$
• Se consideră staţia 1 ca punct de plecare (discoteca).
• Pe toate străzile se poate circula în ambele sensuri.
• Pentru datele de test există întotdeauna soluţie.
• Toate datele de intrare sunt numere naturale.

Exemplu

team.in

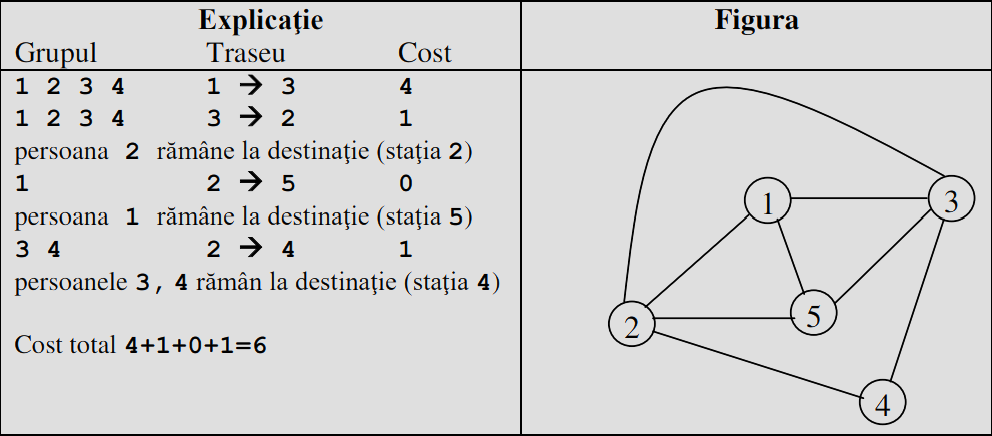
4 
5 
8 
1 2 6
1 3 4
3 4 8
2 4 1
3 5 7
2 3 1
1 5 6
2 5 0
5 2 4 4

team.out

6

Explicație