Problem 2265: ubergraf

În urma succesului internaţional al shgraf-urilor Mirunei, Laura s-a hotarât să lanseze propriul ei tip de graf, numit ubergraf. Un ubergraf este un graf orientat, aciclic, neetichetat, cu proprietatea că mulţimile vecinilor oricăror două vârfuri diferite sunt distincte.
Să considerăm următoarele exemple de grafuri:

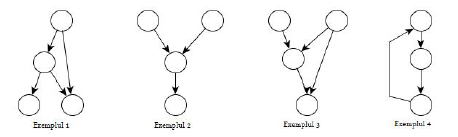
Se observă că primul exemplu nu este un ubergraf, deoarece există două vârfuri a caror mulţime de vecini este mulţimea vidă (cele două vârfuri cu grad extern $0$ ). Nici cel de-al doilea exemplu nu este un ubergraf, deoarece cele două vârfuri cu grad intern $0$ au aceeaşi mulţime de vecini. Cel de-al treilea exemplu este un ubergraf. Ultimul exemplu nu este un ubergraf, pentru că nu este un graf aciclic.
Laura întampină acum o nouă problemă: fiind dat un numar natural $N$ , ar dori dori să ştie câte ubergraf-uri distincte cu $N$ vârfuri există. Cum numărul de ubergraf-uri poate fi foarte mare, ea se mulţumeşte dacă îi spuneţi rezultatul modulo $P$ , unde $P$ este un număr prim dat.

Cerinţă

Determinaţi numărul de ubergraf-uri cu $N$ noduri modulo $P$ .

Date de intrare

Pe prima linie a fişierului de intrare ubergraf.in se află două numere întregi $N$ şi $P$ cu semnificaţia din enunţ.

Date de ieșire

În fişierul de ieşire ubergraf.out se află un singur număr întreg reprezentând numărul cerut.

Restricții și precizări

$1 \leq N \leq 300$
$N < P \leq 30 \ 000$ , $P$ prim
Pentru $65\%$ din teste $N \leq 150$ .
Două ubergraf-uri se consideră distincte dacă nu există nici o bijecţie de la mulţimea vârfurilor în mulţimea vârfurilor astfel încât între două vârfuri să existe arc dacă şi numai dacă există arc între vârfurile corespondente.

Exemplul 1

ubergraf.in

4 37

ubergraf.out

Explicație

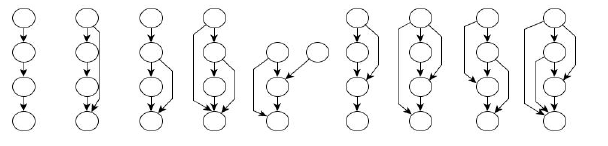
Cele $9$ ubergraf-uri corespunzătoare primului exemplu sunt:

Exemplul 2