Task
You are given a tree of vertices. The tree is a graph such that there is exactly one simple path between every pair of vertices. It's also guaranteed that at least one vertex is directly connected by an edge to at least vertices. One of the vertices is the root, and your task is to find it. In order to do this, you are allowed to ask queries of the following form:
- For a given set of vertices, check if their lowest common ancestor is in this set.
A vertex is a common ancestor of a set of vertices if the paths from all vertices in to the root pass through . The lowest common ancestor (LCA) of a set of vertices is the common ancestor of which is farthest from the root.
Interaction protocol
You must implement one function:
void solve(int n, vector<pair<int,int>> V);
You can call the following functions:
bool query(vector<int> a);
void check(int u);
The function solve will be called exactly once at the beginning of the interaction with two parameters:
- : the number of nodes
- : the edges of the given tree.
The function query may be called by the contestant no more than times. It will return a boolean value true if the LCA (Lowest Common Ancestor) of the nodes is in the given set, and false otherwise.
To check if a node is the root, you can call the check function. After that, the interaction will terminate, and you can't ask any more queries or check for other nodes.
Atention! You must not implement the main function, and must #include the root.h header! You can use global variables and other functions.
Constraints and clarifications
- In the first and second subtask you can ask at most queries.
- In the third subtask, let be the maximum number of queries you asked in any test. If , you will receive all the points for this subtask ( points). Otherwise, you will get points.
| # | Points | Constraints |
|---|---|---|
| 1 | 7 | |
| 2 | 10 | |
| 3 | 83 |
Example
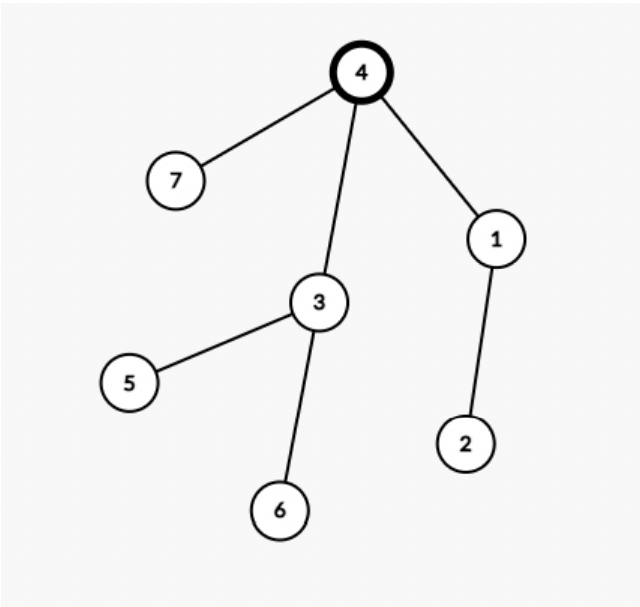
- Grader runs
solve(7, {{4,1},{1,2},{4,3},{3,5},{3,6},{4,7}});. - User calls
query({2, 5, 6});and grader returnsfalse. - User calls
query({3, 6, 3, 5});and grader returnstrue. - User calls
query({2, 1, 7});and grader returnsfalse. - User calls
query({2, 4, 6});and grader returnstrue. - User calls
check(4);and the program ends successfully.
Explanation
The hidden root is vertex .
In the first query, the LCA of vertices and is vertex which is not among vertices and so the answer is false.
In the second query, the LCA of vertices , , and is vertex so the answer is true.
In the third query, the LCA of vertices and is vertex so the answer is false.
In the fourth query, the LCA of vertices and is vertex so the answer is true.
After that, we can guess that root is vertex which is the correct answer.