special

Didel a învățat astăzi la matematică ce este un dreptunghi. El a definit numărul special al unei perechi $(x, y)$ astfel: A desenat un dreptunghi de lungime $x$ și lățime $y$. Numărul special va fi numărul de pătrate (de latură naturală, mai mare ca $1$) incluse în dreptunghiul desenat.

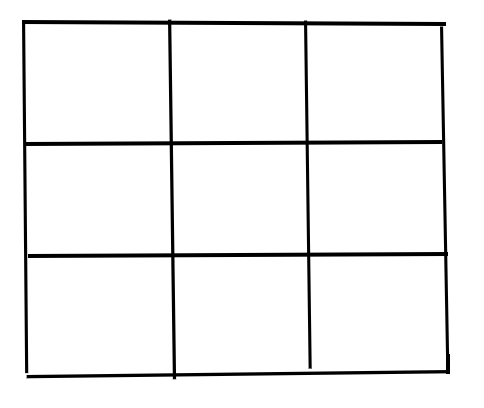
În figura de mai sus, sunt $4$ pătrate de latură $2$ și $1$ pătrat de latură $3$. Deci numărul special al perechii $(3, 3)$ va fi $5$.

Cerință

Se dă un șir de $n$ numere întregi, $a_1, a_2, \dots, a_n$. Se dau $q$ actualizări de forma $l \ r \ x \ y$: Adaugă la $a_l, a_{l + 1}, \dots, a_r$ numărul special al perechii $(x, y)$. După toate actualizările, să se afle maximul din șirul $a$.

Date de intrare

Pe prima linie a fișierului de intrare special.in se găsesc două numere întregi, $n$ și $q$, reprezentând numărul de elemente din șir și numărul de actualizări. Pe a doua linie se vor găsi $n$ numere întregi, separate prin câte un spațiu, $a_1, a_2, \dots, a_n$. Pe următoarele $q$ linii se vor găsi cele $q$ actualizări (pe a $(i + 2)$-a linie se vor găsi numerele $l_i, r_i, x_i, y_i$ (separate prin câte un spațiu), reprezentând forma celei de a $i$-a actualizare).

Date de ieșire

Pe prima linie a fișierului de ieșire special.out se va găsi un singur întreg, maximul din șirul $a$.

Restricții și precizări

• $1 \leq n, q \leq 100 \ 000$
• $1 \leq a_i \leq 10 ^ 9$ (pentru $1 \leq i \leq n$)
• La finalul tuturor actualizărilor, $1 \leq a_i \leq 10 ^ {18}$.
• $1 \leq l_i \leq r_i \leq n$ (pentru $1 \leq i \leq q$)
• $1 \leq x_i, y_i \leq 10 ^ 9$ (pentru $1 \leq i \leq q$)

Exemplu

special.in

5 4
1 2 3 4 5
1 4 6 7
1 2 3 4
4 5 2 1
2 4 5 1

special.out

80

Explicație

Șirul $a$ devine: $79 \ 80 \ 73 \ 74 \ 5$. Maximul este $80$.