A fost o dată un om aşa de sărac, încât unica sa avere era un număr de triunghiuri echilaterale de latură . Aceste triunghiuri aveau proprietatea că se puteau lipi unul de altul de-a lungul unei laturi formând astfel diverse figuri geometrice plane. Împăratul a dat sfoară în ţară că va da jumătate de împărăţie şi pe fata sa de soţie celui care va forma cel mai frumos poligon convex folosind exact triunghiuri echilaterale de latură . Omul nostru a observat că există multe moduri în care pot fi formate poligoane convexe. Totuşi el nu este sigur dacă a calculat bine numărul de poligoane convexe, necongruente două câte două, ce se pot construi cu triunghiurile sale. Acum se teme că a uitat să-l numere exact pe cel dorit de împărat şi că astfel va pierde ocazia de a scăpa de sărăcie şi mai cu seamă de a se căsători cu frumoasa prinţesă.
Cerință
Să se determine numărul poligoanelor convexe, necongruente două câte două care se pot acoperi perfect folosind un număr dat de triunghiuri echilaterale de latură .
Date de intrare
Fişierul de intrare equicover.in conţine pe prima linie numărul natural .
Date de ieșire
Fişierul de ieşire equicover.out va conţine pe prima linie un număr natural reprezentând numărul de poligoane convexe, necongruente două câte două care se pot acoperi perfect folosind triunghiuri echilaterale de latură .
Restricții și precizări
- ;
Exemplu
equicover.in
16
equicover.out
5
Explicație
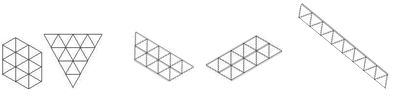
Cele poligoane sunt:

Următoarele poligoane sunt congruente cu unul dintre cele :