Tuscan Peaks

Task

The mountains around Pisa are a well known hiking destination, with a peculiar terrain shape. In particular, you are interested in a rectangular area of $N \times M$ square meters, subdivided into $N \times M$ square cells, each with an area of a square meter.

Those cells are uniquely identified by their distance from the top and the left sides of the rectangle, with cell $(i,j)$ being at a distance of $i$ meters from the top of the map and $j$ meters from the left side of the rectangle.

Each cell $(i, j)$ has an altitude of $H_{i,j}$ meters, described by two arrays of integers $A$ and $B$: $H_{i,j} = A_i\cdot B_j$.
A peak is a cell that has a strictly higher altitude than all the cells that share a side with it.
How many $peaks$ are there?

Input data

The input file consists of:

• a line containing integers $N$, $M$.
• a line containing the $N$ integers $A_{0}, \, \ldots, \, A_{N-1}$.
• a line containing the $M$ integers $B_{0}, \, \ldots, \, B_{M-1}$.

Output data

The output file must contain a single line consisting of 64-bit integer $P$, the number of peaks in the rectangular area.

Constraints and clarifications

• $1 \le N,M \le 10^5$.
• $1 \le A_i \le 10^5$ for each $i=0\ldots N-1$.
• $1 \le B_i \le 10^5$ for each $i=0\ldots M-1$.

Example 1

stdin

1 5
7
4 6 8 5 1

stdout

1

Explanation

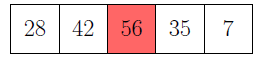
In the first sample case, the altitude of the cells is depicted below, with peaks highlighted in red.

Example 2

stdin

4 5
3 2 8 4
8 5 6 1 3

stdout

6

Explanation

In the second sample case, the altitude of the cells is depicted below, with peaks highlighted in red.