Task
You are given a board of square cells. Each cell contains a tile of one of the following three types:
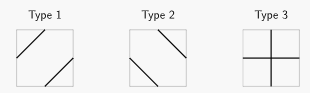
For example, we could have the following configuration:
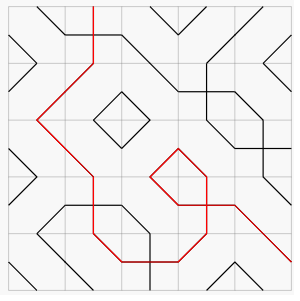
A rope is a maximal connected sequence of segments occurring in the tiling; e.g., a rope is highlighted above in red. (We assume the two segments in type tiles do not touch.) A rope's length is defined as the number of segments it contains; thus, the rope highlighted in red has a length of
. Note that segments from a type cell count the same as segments from type or type cells, even though they are geometrically longer.
You are asked the following:
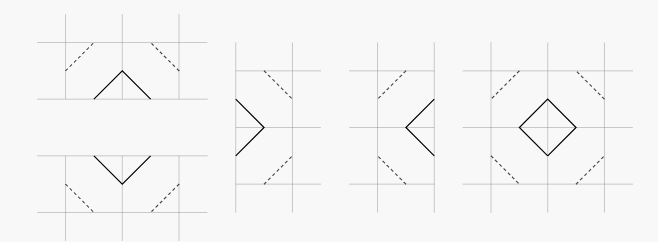
- Compute the number of V-shaped length- ropes with extremities on the edge of the board. Moreover, compute the number of rhombuses, which are defined as length- ropes that do not have extremities on the edge of the board. In other words, find the number of shapes that look like this:
- Compute the length of the longest rope that starts on the edge of the board. For instance, this rope is highlighted in red in the diagram above.
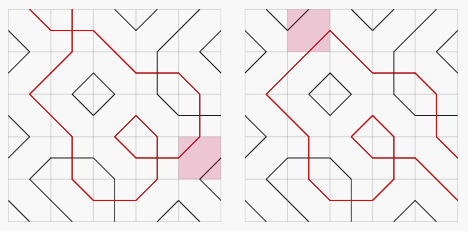
- Change the type of exactly one tile such that the length of the longest rope with extremities on the edge of the board is maximized; also compute the number of ways this can be done to maximize this length. It is guaranteed that a way to change a tile that leads to a longer maximum rope length always exists. For example, replacing one of the highlighted tiles below is optimal for the configuration in the diagram above. The corresponding new longest ropes are again drawn in red.
Input data
On the first line, there are two integers and , representing which of the three problems you should solve ( or ) and the number of rows and columns of the board. The following lines describe the contents of the board, each line describing a row of the board. Tiles on a row are not space-separated.
Output data
Depending on the value of , output the following:
- If , output two integers: the number of V-shaped ropes with extremities on the sides of the board and the number of rhombuses, respectively;
- If , output the length of the longest rope with extremities on the edge of the board;
- If , output two integers: the length of the longest rope with extremities on the edge of the board that can be obtained if the type of exactly one tile is changed and the number of ways of achieving this maximum. Note: if a tile can be changed in two ways to achieve the maximum, it counts as two different ways.
Constraints and clarifications
- For points: .
- For another points: .
- For another points: .
- There are testcases where and testcases where . The values of on these testcases are: .
- The tests for this task are scored individually!
Example 1
stdin
1 5
23211
11232
22123
13232
22312
stdout
5 1
Example 2
stdin
2 5
23211
11232
22123
13232
22312
stdout
16
Example 3
stdin
3 5
23211
11232
22123
13232
22312
stdout
22 2
Example 4
stdin
3 5
22322
12211
12212
21221
11122
stdout
14 4
Explanations
In the first three examples, the board's configuration is as in the first diagram.
For the first example, we count the number of v-shaped ropes of length with extremities on the edge of the board and the number of rhombuses, and output that there are five v-shaped ropes and one rhombus.
For the second example, the longest rope has a length of , as highlighted in the diagram above.
For the third example, we can get a rope length of by changing the highlighted tile. We could also have changed the tile on row and column from type to type ; thus we output that there are two ways of changing a tile so that the maximum length of a rope is .
The fourth example is another board. There are four ways to get to ropes of length .