Time limit: 4s
Memory limit: 256MB
Input: trapezz.in
Output: trapezz.out
Din cauza restricțiilor de buget, minerul Gaudeamus nu a putut să se intoarcă și la această ediție de Moisil++. Prin urmare, el v-a pregătit următoarea urare:
Cerință
Se dau coordonatele a puncte în plan. Găsiți numărul de trapeze isoscele care se pot forma cu punctele date.

este un trapez isoscel dacă:
- nu sunt coliniare
- (altminteri trapezul ar fi un paralelogram).
Date de intrare
Pe prima linie a fișierului de intrare trapezz.in se va afla numărul de puncte .
Pe fiecare dintre următoarele linii se vor afla câte două numere întregi și - coordonatele punctelor date.
Date de ieșire
Fișierul de ieșire trapezz.out va conține numărul de trapeze isoscele care se pot forma cu punctele date.
Restricții și precizări
- ;
- ;
- Toate punctele din fișierul de intrare sunt distincte;
- Atenție la erorile de precizie și la numele fișierelor!;
- Pentru puncte, și ;
- Pentru încă puncte, și ;
- Pentru încă puncte, ;
- Pentru încă de puncte, ;
- Pentru încă de puncte, ;
- Pentru încă puncte, oricare două puncte și au și ;
- Pentru restul de puncte, nu se impun restricții suplimentare.
Exemplul 1
trapezz.in
9
0 0
1 0
2 0
3 0
4 0
0 1
1 1
2 1
4 1
trapezz.out
3
Explicație
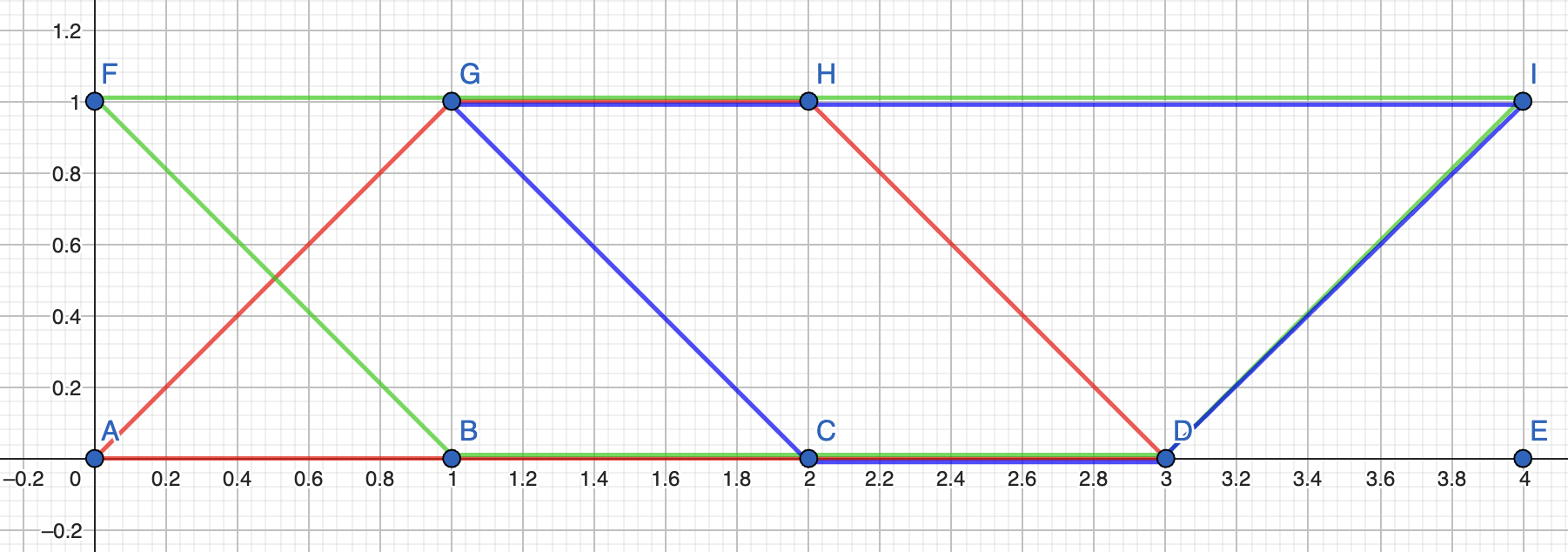
Cele trei trapeze isoscele sunt , și .
Exemplul 2
trapezz.in
11
-3 -3
-3 -2
-2 0
-1 -2
-1 3
1 4
2 -1
2 2
3 0
4 -2
5 1
trapezz.out
7
Explicație
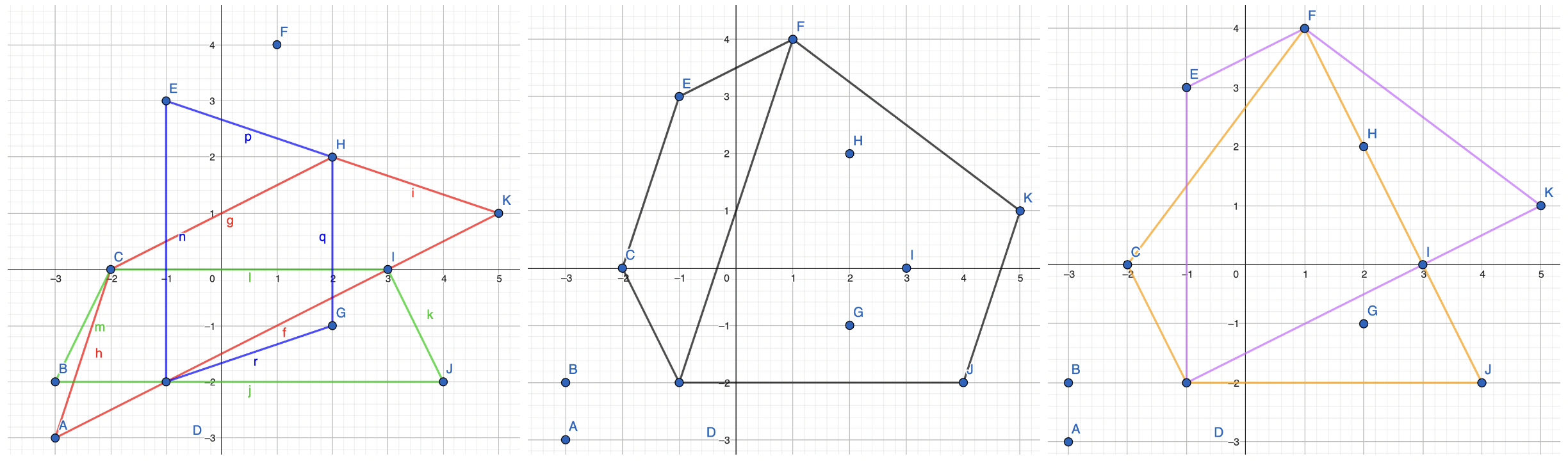
Cele trapeze isoscele sunt: , , , , , și .