tetris

Cerință

Jocul nostru de tetris se desfășoară pe o tablă dreptunghiulară în care piesele “cad” de la linia $1$. La un moment dat unele celule ale tablei sunt ocupate, altele sunt libere, și urmează să “cadă” o nouă piesă.

Din păcate tastele s-au blocat și jucătorul nu mai poate muta piesa sau să o “întoarcă”. Efectiv aceasta cade până atinge partea de jos a tablei sau o parte a sa ajunge imediat deasupra unei celule ocupate. Dacă atunci când piesa se oprește se întâmplă ca una sau mai multe linii să ajungă complet din celule ocupate, aceste linii dispar iar celulele de deasupra acestor linii se translatează în jos pe aceeași coloană, fiecare celulă translatându-se cu numărul de linii cât reprezintă valoarea celor dispărute de sub ea.

Dată fiind configurația tablei și piesa care “cade” să se determine modul în care arată tabla după căderea piesei.

Se garantează că la configurația dată a tablei (înainte de căderea piesei) nu sunt linii cu toate celulele ocupate.

Sunt două tipuri de piese, ambele formate din $h$ celule ocupate:

• Tipul $1$ ($h$ celule ocupate aflate una sub alta):

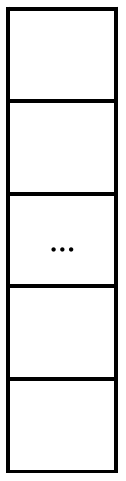
• Tipul $2$ ($h-1$ celule ocupate aflate una sub alta, iar imediat în dreapta celulei de sus mai este încă o ceulă ocupată):

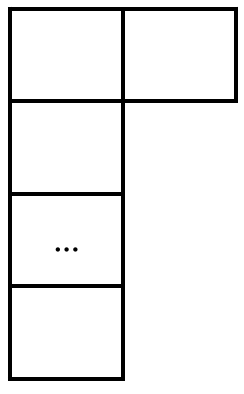
Piesele cad exact pe mijlocul tablei. Dacă lățimea tablei ($m$) este impară “cade” o piesă de tipul $1$, iar dacă lățimea este pară “cade” o piesă de tipul $2$.

Date de intrare

Pe prima linie a fișierului tetris.in se află trei numere $n$, $m$ și $h$, separate prin spațiu, reprezentând respectiv: numărul de linii, numărul de coloane ale tablei dreptunghiulare, precum și numărul de celule pe care le ocupă o piesă, așa cum este descris mai sus.
Pe fiecare din următoarele $n-h$ linii se află câte $m$ valori ce pot fi $0$ sau $1$ ($1$ înseamnă celulă ocupată). Aceste valori sunt separate prin câte un spațiu. Considerăm că deasupra acestor $n-h$ linii mai sunt încă $h$ linii fără nicio poziție ocupată.

Date de ieșire

Fișierul tetris.out va conține configurația tablei de joc fără liniile complet goale de deasupra (fiecare linie afișată va avea câte $m$ elemente $0$ sau $1$, separate prin câte un spațiu).

Restricții și precizări

• $1 \leq n \leq 1 \ 000$;
• $2 \leq m \leq 1 \ 000$;
• $2 \leq h \leq n-1$;
• Pentru $51$ de puncte avem $m$ par;
• Se garantează că pe tablă rămâne la final cel puțin o celulă ocupată.

Exemplu

tetris.in

9 4 5
1 0 0 0
1 0 1 1
1 0 1 1
1 1 0 1

tetris.out

0 1 1 0
1 1 0 0
1 1 0 1

Explicație

Suntem pe cazul cu $m$ par, piesa este de tipul $2$ și cade pe coloanele din mijloc, $2$ și $3$.

Ne imaginăm tabla de joc astfel ($h$ linii libere sus):

0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
1 0 0 0
1 0 1 1
1 0 1 1
1 1 0 1

Căzând, piesa se oprește astfel:

0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 1 1 0
1 1 0 0
1 1 1 1
1 1 1 1
1 1 0 1

Penultimele două linii devin pline cu $1$ și dispar.
Cele $4$ linii rămase pline cu $0$ deasupra nu se mai tipăresc.

0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 1 1 0
1 1 0 0
1 1 0 1