Cerință
O tablă de Monopol de latură este formată din căsuțele de pe marginea unui pătrat de latură :
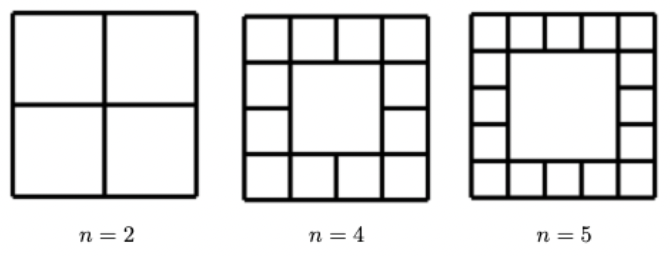
Pe căsuța din colțul din stânga-sus a tablei de Monopol se află un robot care are inițial unități de curent în bateria sa.
În fiecare secundă, robotul poate face una dintre următoarele două acțiuni:
- Robotul va sta pe loc, iar bateria sa se va încărca cu o unitate de curent.
- Dacă bateria robotului are unități de curent, atunci robotul va avansa pe tablă cu căsuțe, iar bateria lui se va descărca cu o unitate.
Dacă , afișați numărul de ture complete pe care le va face robotul dacă nu își poate încarca bateria.
Dacă , afișați numărul minim de secunde de care are nevoie robotul pentru a face o tură completă.
Robotul efectuează o tură completă de fiecare dată când vizitează (inclusiv în trecere) căsuța din colțul din stânga-sus a tablei.
Date de intrare
Pe prima linie a fișierului de intrare monopol.in se va afla numărul cerinței .
Pe a doua linie se vor afla două numere și - dimensiunea tablei de Monopol, respectiv numărul de unități de curent aflate inițial în bateria robotului.
Date de ieșire
Dacă , atunci fișierul de ieșire monopol.out va conține numărul de ture complete pe care le va face robotul dacă nu își poate încarca bateria.
Dacă , atunci fișierul de ieșire monopol.out va conține numărul minim de secunde de care are nevoie robotul pentru a face o tură completă.
Restricții și precizări
- ;
- ;
- ;
- Pentru puncte, și ;
- Pentru încă puncte, ;
- Pentru puncte, și ;
- Pentru încă de puncte, și ;
- Pentru încă de puncte, și ;
- Pentru încă puncte, .
Exemplul 1
monopol.in
1
2 2
monopol.out
0
Explicație
Robotul nu va face nicio tură completă:
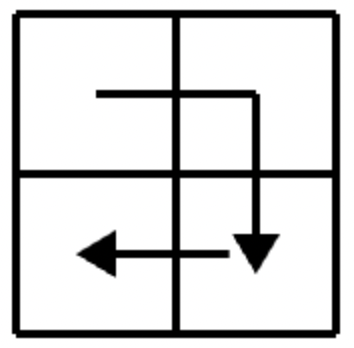
Exemplul 2
monopol.in
1
4 5
monopol.out
1
Explicație
Robotul va face o singură tură completă:
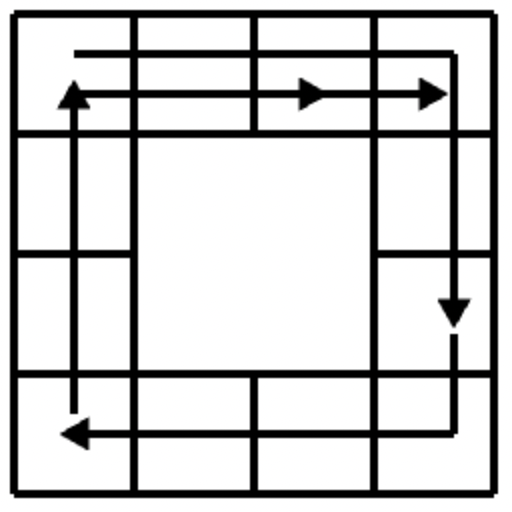
Exemplul 3
monopol.in
1
4 8
monopol.out
3
Explicație
Robotul se va mișca în față cu căsuțe.
Deoarece o tablă de latură are căsuțe, robotul va face ture complete.
Exemplul 4
monopol.in
2
5 6
monopol.out
4
Explicație
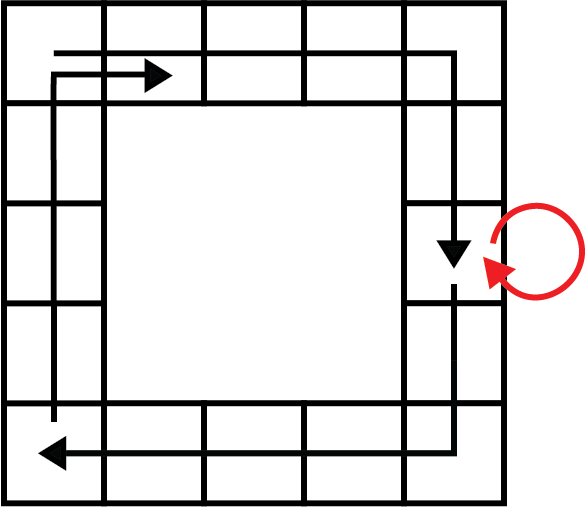
În prima secundă, robotul va înainta cu căsuțe, iar bateria sa se va descărca cu o unitate.
În a doua secundă, robotul își va încărca bateria.
În a treia secundă, robotul va înainta cu căsuțe, iar bateria sa se va descărca cu o unitate.
În a patra secundă, robotul va înainta cu căsuțe, iar bateria sa se va descărca cu o unitate.
Exemplul 5
monopol.in
2
2 2
monopol.out
3
Explicație
În prima secundă, robotul își va încărca bateria cu o unitate.
În a doua secundă, robotul va înainta cu căsuțe, iar bateria sa se va descărca cu o unitate.
În a treia secundă, robotul va înainta cu căsuțe, iar bateria sa se va descărca cu o unitate.
Exemplul 6
monopol.in
2
7 0
monopol.out
12
Exemplul 7
monopol.in
2
1000000 0
monopol.out
4899
Exemplul 8
monopol.in
2
1000000000000 0
monopol.out
4898979