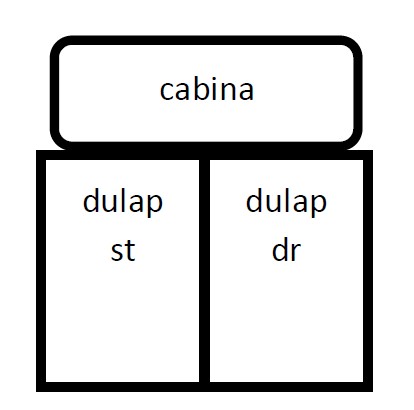
Maxi a deschis un magazin de mobilă secănd şi are multe comenzi de dulapuri pe care le transportă cu o maşină învechită (e o maşină secănd). Maşina este concepută special pentru a transporta dulapuri grele. Remorca maşinii este împărţită în două părţi aşa cum arată în figura alăturată. Maşina e aşa de veche încât dacă timp de zile consecutive o parte a maşinii (stânga sau dreapta) este folosită continuu, se rupe osia pe acea parte. În continuare spunem că rezistenţa maşinii este . Maşina poate transporta , sau dulapuri pe zi şi transporturile vor fi planificate în aşa fel ca maşina să nu se strice.
În oraşul lui Maxi o săptămână are zile, iar comenzile de transport se repetă identic în fiecare săptămână. De exemplu: rezistenţa maşinii este , o săptămână are zile, iar comanda săptămânală distribuită pe zile este: .
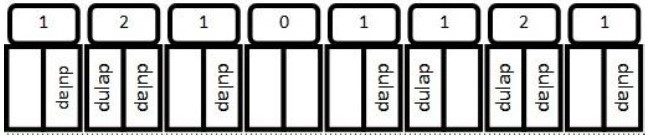
Planificarea pe zile de mai jos e corectă pentru că nicio parte a maşinii nu va transporta dulapuri zile consecutive:
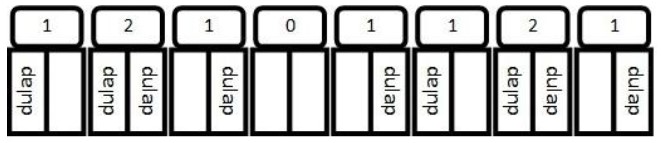
Planificarea următoare e greşită pentru că în primele trei zile maşina va transporta pe partea dreaptă dulapuri:
Cerinţă
Aflați în câte moduri modulo se pot planifica transporturile pe zile date, dacă se cunoaşte rezistenţa a maşinii, numărul al zilelor din săptămână, respectiv şirul comenzilor săptămânale.
Date de intrare
Fişierul marfa.in conţine pe prima linie două numere naturale şi cu semnificaţiile de mai sus. Pe linia a doua se găseşte numărul al zilelor din săptămână. Pe linia a treia sunt scrise numere naturale de valori , sau separate prin spaţiu, reprezentând comanda săptămânală de mobilă.
Date de ieşire
Fişierul marfa.out va conţine un singur număr natural, numărul planificărilor corecte distincte modulo .
Restricţii şi precizări
Exemplu
marfa.in
6 3
5
1 0 2 2 0
marfa.out
4
Explicație
Se cere numărul planificărilor pe zile, cu rezistenţa maşinii zile. Săptămâna are zile.
Pentru comanda avem planificări posibile (comanda din ziua este , la fel ca şi prima zi, pentru că se reia săptămâna:
