poligon

Cerință

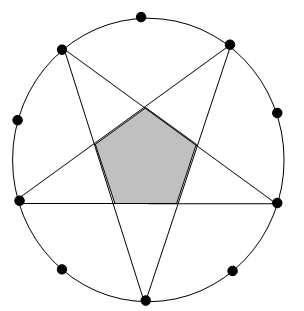
Geo a învăţat o metodă de a fixa $n$ puncte pe un cerc de rază $r$, astfel încât să împartă cercul în $n$ coarde egale ca lungime. Apoi şi-a ales un număr $k$ şi a început să unească punctele succesiv, din $k$ în $k$, păstrând acelaşi sens, până ce a ajuns în punctul din care a pornit. Astfel, dacă a fixat $n=10$ puncte pe cerc pe care le-a numerotat $1, 2, \dots, 10$ (vezi figura) şi şi-a ales $k=6$, atunci el uneşte punctul $1$ cu $7$, apoi pe $7$ cu $3$, apoi $3$ cu $9$, apoi $9$ cu $5$, şi în sfârşit $5$ cu $1$.
Apoi a colorat poligonul format în interior, pornind din centrul cercului şi fără a depăşi vreuna dintre liniile desenate. El se întreabă în final câte laturi are poligonul colorat şi care este aria acestuia.

Pentru $n$, $k$ şi $r$ numere naturale date, se cere numărul de laturi $L$ ale poligonului colorat şi aria $S$ a acestuia (cu $2$ zecimale exacte).

Date de intrare

Din fişierul poligon.in se citesc trei numere naturale $n$, $k$ şi $r$ despărţite prin câte un spaţiu.

Date de ieșire

În fişierul poligon.out se scriu, pe linii diferite două valori: pe prima linie numărul $L$ de laturi ale poligonului colorat, iar pe linia a doua numărul real reprezentând aria acestuia.

Restricții și precizări

• $3 < n < 10 \ 001$ număr natural
• $0 < k < n$ număr natural
• pentru $n$ par, $2 \cdot k \neq n$
• $10 < r < 501$
• Pentru fiecare test, dacă numărul de laturi determinat este corect, primiţi $20\%$ din punctajul maxim de pe testul respectiv. În plus, dacă şi aria determinată este corectă, primiţi punctajul maxim.
• Aria este considerată corectă dacă modulul diferenţei dintre rezultatul corect şi cel furnizat de concurent nu depăşeşte $0.0001$.
• Pentru $70\%$ din testele folosite la evaluare, $n < 501$

Exemplul 1

poligon.in

10 6 100 

poligon.out

5
3468.9319

Exemplul 2

poligon.in

30 13 200

poligon.out

30
5452.0431