Definim mulțimea punctelor laticiale ordonate ca fiind mulțimea perechilor de puncte din plan cu proprietățile: și sunt numere naturale și .
Cerinţă
Considerând un număr natural , să se scrie un program care determină numărul al triunghiurilor distincte ce îndeplinesc simultan condițiile:
- unul din vârfurile triunghiului este punctul de coordonate ;
- celelalte două vârfuri se gâsesc în două puncte laticiale ordonate cu ambele coordonate ;
- în interiorul sau pe marginea triunghiului nu se mai găsesc alte puncte laticiale ordonate.
Exemple
- pentru , există următoarele triunghiuri, deci .
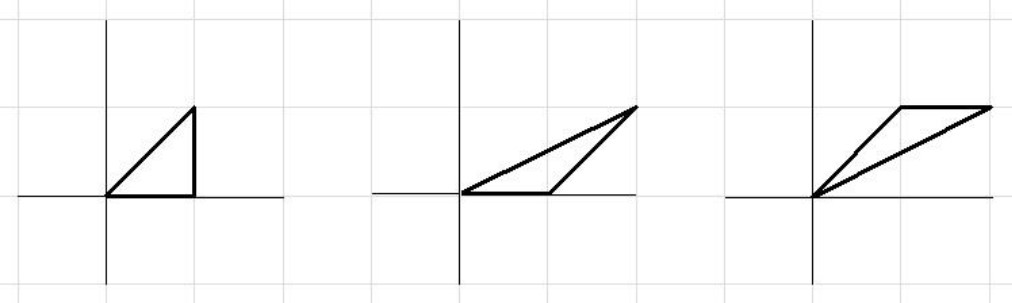
- pentru , există următoarele triunghiuri, deci .

Date de intrare
Fişierul de intrare emptri.in conţine pe prima linie numărul natural , cu semnificaţia de mai sus.
Date de ieşire
Fişierul de ieşire emptri.out va conţine pe prima linie numărul natural .
Restricţii şi precizări
- ;
- Două puncte laticiale ordonate și sunt distincte dacă sau ;
- Două triunghiuri sunt distincte dacă diferă prin cel puțin un punct laticial asociat vârfurilor.
Exemplul 1
emptri.in
2
emptri.out
3
Explicație
. Există triunghiuri având un vârf în origine și celelalte două în puncte laticiale ordonate de coordonate , ce nu mai conțin în interior sau pe margine alte puncte laticiale ordonate.
Exemplul 2
emptri.in
3
emptri.out
7
Explicație
. Există triunghiuri având un vârf în origine și celelalte două în puncte laticiale ordonate de coordonate , ce nu mai conțin în interior sau pe margine alte puncte laticiale ordonate.